FINDING THE VALUE OF N IN PERMUTATION

Example 1 :

If ^{(n - 1)} P₃ : ⁿ P ₄  =  1 : 10, find the value of n.

Solution :

ⁿP_r  =  n!/(n-r)!

[(n-1)!/(n-4)!] / [n!/(n-4)!]  =  (1/10)

[(n-1)!/(n-4)!] ⋅ [(n-4)!/n!]  =  (1/10)

[(n-1)!/n(n-1)!]  =  (1/10)

1/n  =  1/10

n  =  10

Hence the value of n is 10.

Example 2 :

If ¹⁰P_r−1 =  2 ⋅ ⁶P_r, find r.

Solution :

10!/(11-r)!  =  2 ⋅ (6!/(6-r)!)

10⋅9⋅8⋅7⋅6!/(11-r)(10-r)(9-r)(8-r)(7-r)(6-r)!  =  2⋅(6!/(6-r)!)

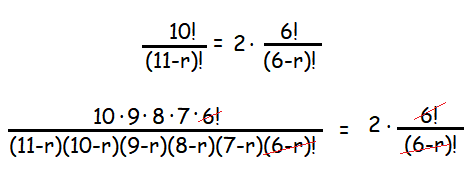
10⋅9⋅8⋅7/(11-r)(10-r)(9-r)(8-r)(7-r)  =  2

(11-r)(10-r)(9-r)(8-r)(7-r)  =  10⋅9⋅4⋅7

(11-r)(10-r)(9-r)(8-r)(7-r)  =  5 ⋅ 2 ⋅ 3 ⋅ 3 ⋅ 4 ⋅ 7

(11-r)(10-r)(9-r)(8-r)(7-r)  =  7 ⋅ 6 ⋅ 5 ⋅ 4 ⋅ 3

11 - r  =  7

11 - 7  =  r

r  =  4

Hence the value of r is 4.

Example 3 :

(i) Suppose 8 people enter an event in a swimming meet. In how many ways could the gold, silver and bronze prizes be awarded?

(ii) Three men have 4 coats, 5 waist coats and 6 caps. In how many ways can they wear them?

Solution :

(i) 8 people have equal chances to get 1st prize gold, 7 people are having equal chances of getting the 2nd prize silver, 6 people are having equal chances of getting 3rd prize.

Hence the total number of ways  =  8 ⋅ 7 ⋅ 6

  =  336 ways

(ii) Three men have 4 coats, 5 waist coats and 6 caps. In how many ways can they wear them?

Solution :

1^st man can wear any of the 4 coats.
2^nd man can wear any of the remaining 3 coats.
3^rd man can wear any of the remaining 2 coats.

So, number of ways in which 3 men can wear 4 coats 

  =  4 ⋅ 3⋅ 2 

  =  24

Similarly,

Number of ways in which 3 men can wear 5 waistcoats 

  =  5 ⋅ 4 ⋅ 3

  =  60

Number of ways in which 3 men can wear 6 caps

  =  6 ⋅ 5 ⋅ 4

  =  120

Hence, required number of ways

  =  24 ⋅ 60 ⋅ 120

  =  172800

Hence the total number ways is 172800.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.