PRIME FACTORIZATION
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Expressing a composite number (e.g. 4, 18, 35, 49, 64, 128, etc.) as a product of factors that are all prime numbers is called the prime factorization.
For example, you can write the composite number 36 as product of factors as shown below.
36 = 1 x 36
36 = 2 x 18
36 = 3 x 12
36 = 4 x 9
36 = 6 x 6
You can find the factors of 36 easily as 1, 2, 3, 4, 6, 9, 12, 18 and 36. Note that not all the factors of 36 are prime numbers.
To find the prime factors of 36, we do the prime factorization by the following methods.
1. Division Method
2. Factor Tree Method
Division Method
Using Division Method, we can find the prime factorization of 36 as follows :
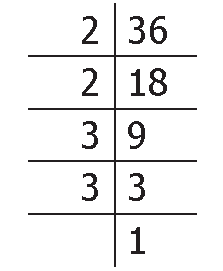 36 = 2 x 2 x 3 x 3 |
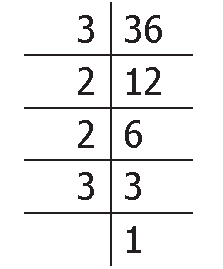 36 = 3 x 2 x 2 x 3 |
When we find prime factors of 36, why do we start with 2 or 3 ? why don't we start with 5 ?
Since 36 is not a multiple of 5, it is not divisible by 5. So, to find the prime factors of a composite number, it will be useful to check for divisibility by smaller numbers like 2, 3 and 5 first and not take numbers at random.
Factor Tree Method
You can find the prime factors of the same composite number 36 using Factor Tree Method as shown below.
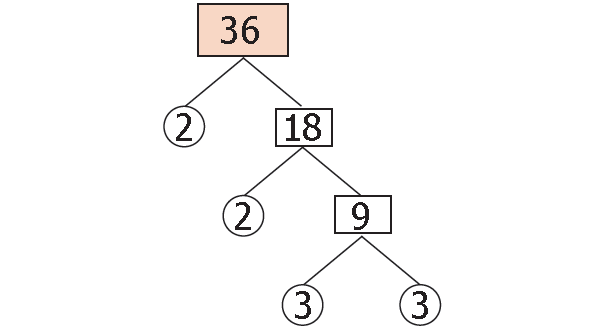
Prime factorization of 36 :
36 = 2 x 2 x 3 x 3
In each step, you have to put a prime factor (e.g. 2, 3, 5, 7, 11, 13, etc.) into the CIRCLE and the other factor into the BOX .
In the next step, you have to factor the number in the BOX by putting one of its prime factors into the CIRCLE and the other factor into the BOX .
You have to continue until you reach a number which has only two prime factors and put each of them into a CIRCLE.
Then, write down all of the factors in the CIRCLES and that is your prime factorization of the original number.
Examples
1) Find the prime factors of 900 using division method.
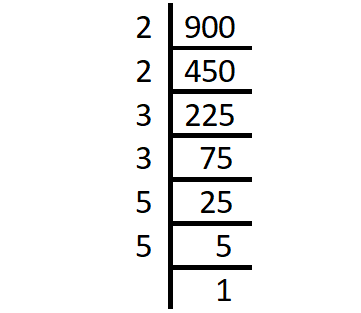
Prime factorization of 900 :
900 = 2 x 2 x 3 x 3 x 5 x 5
2) Find the prime factors of 625 using division method.
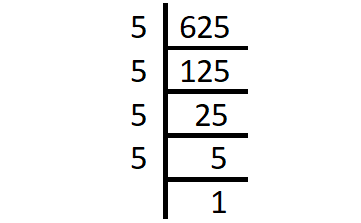
Prime factorization of 625 :
625 = 5 x 5 x 5 x 5
3) Find the prime factors of 18, 24 and 30 by factor tree method.
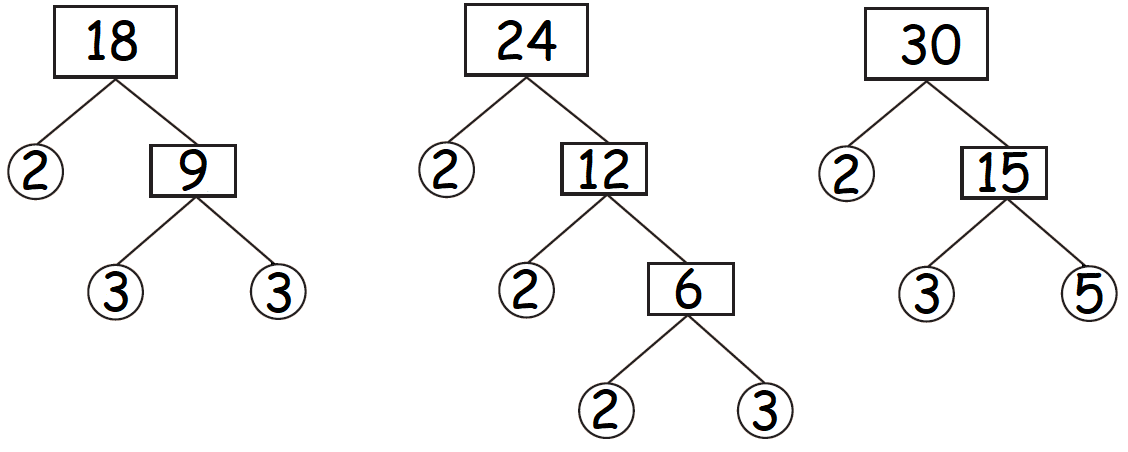
Prime factorization of 18 :
18 = 2 x 3 x 3
Prime factorization of 24 :
24 = 2 x 2 x 2 x 3
Prime factorization of 30 :
30 = 2 x 3 x 5
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com
Recent Articles
-
Quantitative Reasoning Questions and Answers
Dec 14, 25 06:42 AM
Quantitative Reasoning Questions and Answers -
Specifying Units of Measure
Dec 14, 25 06:38 AM
Specifying Units of Measure -
Coin Tossing Probability
Dec 13, 25 10:11 AM
Coin Tossing Probability - Concept - Sample Space - Formula - Solved Problems