FINDING THE PERIMETER OF A TRIANGLE

Let a, b and c is the sides of the triangle. Then, the perimeter

P = a + b + c

Example 1 :

The sides of a triangle are 12 cm, 6 cm and 8 cm, find the perimeter of the triangle.

Solution :

Let a, b and c are the three sides of the triangle

a  =  12 cm, b  =  6 cm and c  =  8 cm

Perimeter P  =  12+6+8

=  26 cm

Therefore the perimeter of a required triangle  =  26 cm.

Example 2 :

The sides of a triangle are 5 cm, 7 cm and 9 cm find the perimeter of the triangle.

Solution :

Let a, b and c are the three sides of the triangle

a = 5 cm, b = 7 cm and c = 9 cm

Perimeter P  =  5+7+9

=  21 cm

Therefore the perimeter of a required triangle  =  21 cm.

Example 3 :

The sides of a triangle are in the ratio 2x, 3x and 5x. If the perimeter of the triangle is 100 then find the measurement of three sides.

Solution :

Let a, b and c be the three sides of the triangle

a  =  2x, b  =  3x  and c  =  5x

Perimeter P  =  2x+3x+5x

=  10 x

Perimeter of triangle  =  100 cm

10x  =  100

x  =  10 cm

Therefore, a  =  2x  =  2(10)  =  20 cm

b  =  3x  =  3(10)  =  30 cm

c  =  5x  =  5(10)  =  50 cm

Example 4 :

The sides of a triangles are in the ratio of 1/2 : 1/3 : 1/4. If the perimeter is 52 cm, then the length of the smallest side is.

Solution :

Ratio of sides of triangle 1/2 : 1/3 : 1/4 to be changed as 6 : 4 : 3

So, side lengths will be 6x, 4x and 3x.

Perimeter  =  52

(6x+4x+3x)/12  =  52

13x/12  =  52

x  =  52(12/13)

x  =  48

So, the smallest side will be 48/2  =  24 cm.

Example 5 :

The area of a triangle is 216 cm² and its sides are in the ratio 3 : 4 : 5. The perimeter of the triangle is :

Solution :

Let sides be 3x, 4x and 5x.

Area of triangle  =  √s(s-a)(s-b) (s-c)

s  =  (3x+4x+5x)/2

s  =  12x/2

s  =  6x

s - a = 6x - 3x = 3x

s - b = 6x - 4x = 2x

s - c = 6x - 5x = x

√6x(3x)(2x) (x)  =  216

3x(2x)  =  216

6x²  =  216

x²  =  36

x  =  6

So, side lengths are 18 cm, 12 cm and 6 cm.

Perimeter of the triangle = 18 + 12 + 6

= 36 cm

Example 6 :

Area of a right triangle is 54 cm². If one of its legs is 12 cm long, its perimeter is

Solution :

Area of right triangle = 54 cm²

(1/2) x base x height = 54

let height of the triangle = 12 cm

(1/2) x base x 12 = 54

base x 6 = 54

base = 54/6

base = 9

Hypotenuse = √9² + 12²

= √81 + 144

= √225

= 15

Perimeter of triangle = 12 + 9 + 15

= 36 cm

So, the required perimeter is 36 cm.

Example 7 :

Perimeter of triangle ABC = Perimeter of triangle PQR. Find area of triangle ABC.

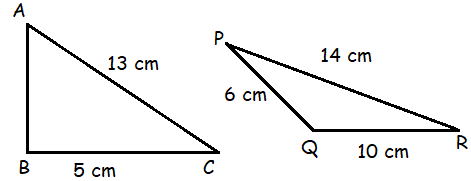
Solution :

Given that,

Perimeter of triangle ABC = Perimeter of triangle PQR

Perimeter of triangle PQR = PQ + QR + PR

= 6 + 10 + 14

= 30 cm

Perimeter of triangle ABC = AB + BC + CA

30 = AB + 5 + 13

30 = AB + 18

AB = 30 - 18

AB = 12 cm

Base of triangle BC = 5 cm and height of triangle = 12 cm

= (1/2) x base x height

= (1/2) x 5 x 12

= 5 x 6

= 30 cm²

Example 8 :

Area of an isosceles triangle is 48 cm². If the altitudes corresponding to the base of the triangle is 8 cm, find the perimeter of the triangle.

Solution :

Since it is isosceles triangle, two sides will be equal.

Let x be the measure of equal sides.

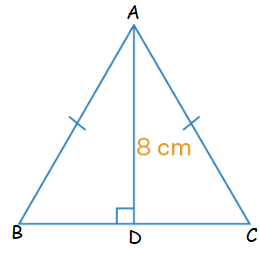
(1/2) x base x height = 48

Given that, base = 8 cm

(1/2) x base x 8 = 48

base x 4 = 48

base (BC) = 12

BD = 6 cm

AB² = AD² + BD²

AB² = 8² + 6²

AB² = 64 + 36

AB² = 100

AB = 10 cm

Perimeter of triangle = AB + BC + CA

= 10 + 12 + 10

= 32

So, the required perimeter is 32 cm

Area of triangle PQR is 100 cm².  If altitude QN is 10 cm, then its base PR is

(a) 20 cm     (b) 15 cm     (c) 10 cm      (d) 5 cm

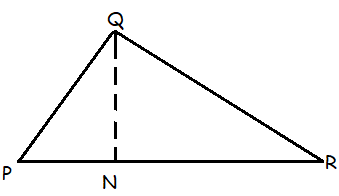
Solution :

Area of triangle = (1/2) x base x height

20 = (1/2) x PR x QN

40 = PR x QN

Applying the value of QN, we get

40 = PR z 10

PR = 40 / 10

PR = 4 cm

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.