FINDING THE COORDINATES OF POINT OF TRISECTION

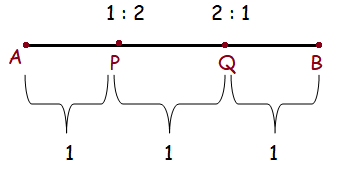
Question 1 :

Find the coordinates of the points of trisection of the line segment joining the points A(−5, 6) and B(4,−3).

Solution :

=  (mx₂ + nx₁)/(m + n), (my₂ + ny₁)/(m + n)

Point P divides the line segment in the ratio 1 : 2

A(−5, 6) and B(4,−3)

=  (1(4) + 2(-5))/(1 + 2), (1(-3) + 2(6))/(1 + 2)

=  (4 - 10)/3, (-3 + 12)/3

=  -6/3, 9/3

=  (-2, 3)

Point Q divides the line segment in the ratio 2 : 1

A(−5, 6) and B(4,−3)

=  (2(4) + 1(-5))/(2 + 1), (2(-3) + 1(6))/(1 + 2)

=  (8 - 5)/3, (-6 + 6)/3

=  3/3, 0/3

=  (1, 0)

Question 2 :

The line segment joining A(6,3) and B(−1, −4) is doubled in length by adding half of AB to each end. Find the coordinates of the new end points.

Solution :

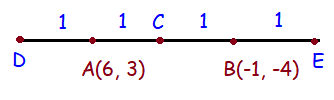
To find the half of the length of AB, we have to find the midpoint of the line segment AB.

Let C be the point which divides the line segment AB in the ratio 1 : 1 

  =  (mx₂ + nx₁)/(m + n), (my₂ + ny₁)/(m + n)

  =  (1(-1) + 1(6))/(1 + 1), (1(-4) + 1(3))/(1 + 1)

  =  (-1 + 6)/2, (-4 + 3)/2

  =  (5/2, -1/2)

A is the point which divides the line segment in the ratio 1 : 2 internally.

A(6, 3)  =  (mx₂ + nx₁)/(m + n), (my₂ + ny₁)/(m + n)

(1(-1) + 2x₁)/(1 + 2), (1(-4) + 2y₁)/(1 + 2)  =  (6, 3)

(-1 + 2x₁)/3, (-4 + 2y₁)/3  =  (6, 3)

Equating the x and y -coordinates 

Hence the point D is (19/2, 13/2).

B is the point which divides the line segment in the ratio 2 : 1 internally.

B(-1, -4)  =  (2x₂ + 1(6))/(2 + 1), (2y₂ + 1(3))/(2 + 1)

 (2x₂ + 6)/3, (2y₂ + 3)/3  =  B(-1, -4)

Equating the x and y -coordinates 

Hence the point E is (-9/2, -15/2).

Question 3 :

Find the coordinates of point of trisection of the segment joining points (4, -8) and (7, 4).

Solution :

In the trisection, the first point will divide the line segment joining the above points in the ratio of 1 : 2.

Let A and B be the required points.

Using section formula,

= (1(7) + 2(4)) / (1 + 2), (1(4) + 2(-8)) / (1 + 2)

= (7 + 8)/3, (4 - 16)/3

= 15/3, -12/3

= A(5, -4)

So, the point A (5, -4).

In the trisection, the second point will divide the line segment joining the above points in the ratio of 2 : 1.

Using section formula,

= (2(7) + 1(4)) / (2 + 1), (2(4) + 1(-8)) / (2 + 1)

= (14 + 4)/3, (8 - 8)/3

= 18/3, 0/3

= (6, 0)

So, the point B is (6, 0).

Question 4 :

If A (5, -1), B (-3, -2) and C (-1, 8) are vertices of triangle ABC, find the length of median through A and find the coordinates of the centroid.

Solution :

A (5, -1), B (-3, -2) and C (-1, 8)

Centrod of the triangle = (x₁ + x₂ + x₃)/3, (y₁ + y₂ + y₃)/3

= (5 - 3 - 1)/3, (-1 - 2 + 8)/3

= (5 - 4)/3, (-3 + 8)/3

= Centroid (1/3, 5/3)

Midpoint of BC :

B (-3, -2) and C (-1, 8)

= (-3 - 1)/2, (-2 + 8)/2

= -4/2, 6/2

= (-2, 3)

Endpoint of median through A is (5, -1) and (-2, 3).

distance between these two points

= √(x₂ - x₁)² + (y₂ - y₁)²

= √(-2 - 5)² + (3 + 1)²

= √(-7)² + 4²

= √49 + 16

= √65

So, the length of median through A is √65.

Question 5 :

The line joining the points (2, 1) and (5, 8) is trisected at the points P and Q. If point P lies on the line 2x - y + k = 0, find the value of k ?

Solution :

Since the given points are trisected by the points P and Q, the point P will divide the line segment in the ratio of 1 : 2.

= (lx₂ + mx₁)/(l + m), (ly₂ + my₁)/(l + m)

= (1(5) + 2(2))/(1 + 2), (1(8) + 2(1))/(1 + 2)

= (5 + 4)/3, (8 + 2)/3

= (9/3, 10/3)

= (3, 10/3)

2x - y + k = 0

Since the point (3, 10/3) lies on the line 2x - y + k = 0, we apply this point.

2(3) - (10/3) + k = 0

6 - (10/3) + k = 0

8/3 + k = 0

k = -8/3

So, the value of k is -8/3.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.