FINDING THE CENTER OF A CIRCLE

Problem 1 :

Which of the following equations represents the equation of the circle shown in the -xy plane above?

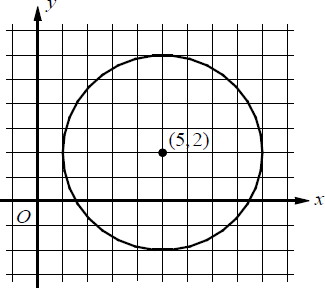
a)  (x + 5)² + (y + 2)² = 4         b)  (x - 5)² + (y - 2)² = 4

c)  (x + 5)² + (y + 2)² = 16       d)  (x - 5)² + (y - 2)² = 16

Solution :

By observing the circle above, the center of the circle is (5, 2). One of the points on the circle is (1, 2)

Distance between these two points = radius

√(x₂ - x₁)² + (y₂ - y₁)²

= √(1 - 5)² + (2 - 2)²

= √(-4)² + 0²

Radius = 4

Equation of circle with the center (h, k) and radius r is :

(x - h)² + (y - k)² = r²

(x - 5)² + (y - 2)² = 4²

(x - 5)² + (y - 2)² = 16

So, option d is correct.

Problem 2 :

 (x − 8)² + (𝑦 − 6)² = 36

For the equation above, what is the coordinate point for the center of the circle as well as the circle’s radius?

a) Center: (-8, -6), Radius: 36

b) Center: (8, 6), Radius: 36

c) Center: (-8, -6), Radius: 6

d) Center: (8, 6), Radius: 6

Solution :

Comparing the given equation

 (x − 8)² + (𝑦 − 6)² = 36

with

(x - h)² + (y - k)² = r²

we know that, (h, k) is (8, 6) and  r² = 36

So, the center of the circle is (8, 6) and radius is 6.. Option d is correct.

Problem 3 :

x² + 10x + y² – 6y = -18

The graph of the equation shown above is a circle. What is the radius of the circle?

a) 3     b) 4      c) 5      d) 9

Solution :

x² + 10x + y² – 6y = -18

x² + 10x + y² – 6y + 18 = 0

x² + 2(x)(5) + y² – 2(3)(y) + 18 = 0

x² + 2(x)(5) + 5² + y² – 2(3)(y) + 3² + 18 - 5² - 3²  = 0

(x + 5)² + (y - 3)² = -18 + 25 + 9

(x + 5)² + (y - 3)² = 16

Comparing r² and 16

Radius of the circle is 4 units.

Problem 4 :

x² + 18x + y² – 8y = -48

The graph of the equation shown above is a circle. What is the radius of the circle?

a) 4      b) 5      c) 6      d) 7

Solution :

x² + 18x + y² – 8y = -48

x² + 18x + y² – 8y + 48 = 0

x² + 2(x)(9) + y² – 2(4)(y) + 48 = 0

x² + 2(x)(9) + 9² + y² – 2(4)(y) + 4² + 48 - 9² - 4²  = 0

(x + 9)² + (y - 4)² = -48 + 81 + 16

(x + 9)² + (y - 4)² = 49

Comparing r² and 49

Radius of the circle is 7 units.

Problem 5 :

x² - 4x +  y² + 6y = 87

The graph of the equation shown above is a circle. What is the coordinate point of the center of the circle?

a) (13, 10)    b) (4, 13)    c) (-4, 6)    d) (2, -3)

Solution :

x² - 4x +  y² + 6y = 87

x² - 4x +  y² + 6y - 87 = 0

x² - 2(x)(2) +  y² + 2(3)(y) - 87 = 0

x² - 2(x)(2) + 2² +  y² + 2(3)(y) + 3² - 87 - 2² - 3² = 0

(x - 2)² +  (y + 3)² - 87 - 4 - 9 = 0

(x - 2)² +  (y + 3)² - 100 = 0

(x - 2)² +  (y + 3)² = 100

Comparing the given equation

(x - 2)² +  (y + 3)² = 100

with

(x - h)² + (y - k)² = r²

we know that, (h, k) is (2, -3) and  r² = 100

So, the required center is (2, -3).

Problem 6 :

The circle has the center at the point (4, 3) and passes through the point (0, 0), which of the following points also lie on the circle.

a)  (1, -1)    b)  (5, -2)   c)  (-2, 4)      d)   (7, 7)   e)  (8, 6)

Solution :

Center of the circle is (4, 3) and a point lies on the circle is (0, 0).

(x - h)² + (y - k)² = r²

(x - 4)² + (y - 3)² = r²

Since it passes through the point (0, 0), we get

(0 - 4)² + (0 - 3)² = r²

16 + 9 = r²

 r² = 25

(x - 4)² + (y - 3)² = 25

To check if the point (1, -1) lies on the circle, we apply

(1 - 4)² + (-1 - 3)² = 25

(-3)² + (-4)² = 25

9 + 16 = 25

25 = 25

Since the point satisfies the equation of circle, we understand the point (1, -1) lies on the circle.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.