FINDING THE AREA OF A COMPOSITE FIGURE WORKSHEET

Problem 1 :

Find the area of the figure given below.

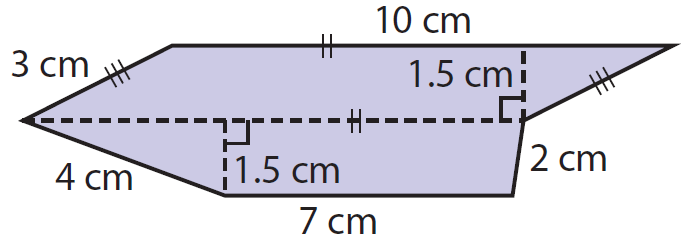
Solution :

Step 1 :

Separate the figure into smaller, familiar figures: a parallelogram and a trapezoid.

Step 2 :

Find the area the parallelogram.

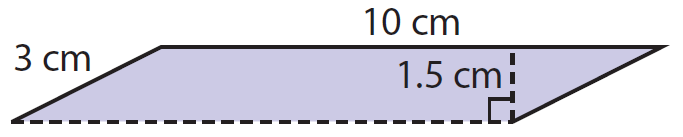
Base (b) = 10 cm

Height (h) = 1.5 cm

Use the formula.

A = bh

A = 10 · 1.5

= 15

The area of the parallelogram is 15 square cm.

Step 3 :

Find the area the trapezoid.

Base₁ (b₁) = 7 cm

Base₂ (b₂) = 10 cm

Height (h) = 1.5 cm

Use the formula.

A = (1/2)h(b₁ + b₂)

= (1/2)(1.5)(7 + 10)

= (1/2)(1.5)(17)

= 12.75

The area of the trapezoid is 12.75 square cm.

Step 4 :

Add the areas to find the total area.

A = 15 + 12.75

= 27.75

So, the area of the given composite figure is 27.75.

Problem 2 :

Find the area of the figure given below.

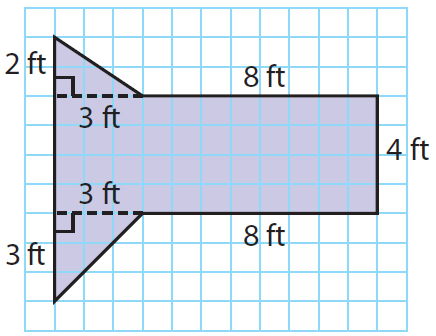
Solution :

Step 1 :

Separate the figure into smaller, familiar figures: a two triangles and a rectangle.

Step 2 :

Find the area the first triangle.

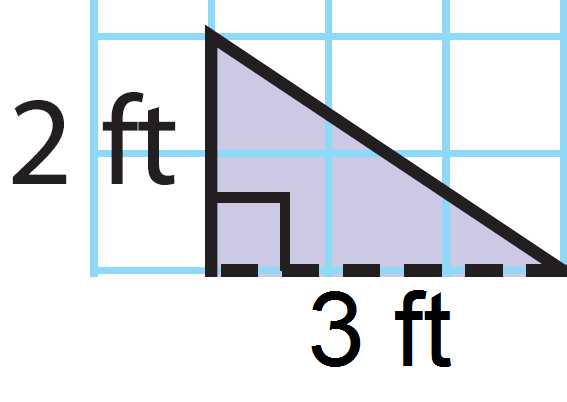
Base (b) = 3 ft

Height (h) = 2 ft

Use the formula.

A = (1/2)bh

= (1/2)(3)(2)

= 3

The area of the first triangle is 3 square ft.

Step 3 :

Find the area the rectangle.

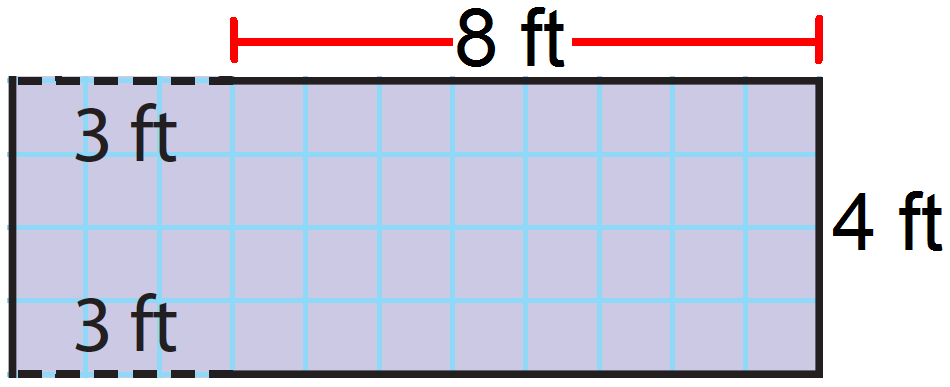
Length (l) = 8 + 3  =  11 ft

Height (h) = 4 ft

Use the formula.

A = l x w

= 11 x 4

= 44

The area of the rectangle is 44 square ft.

Step 4 :

Find the area the second triangle.

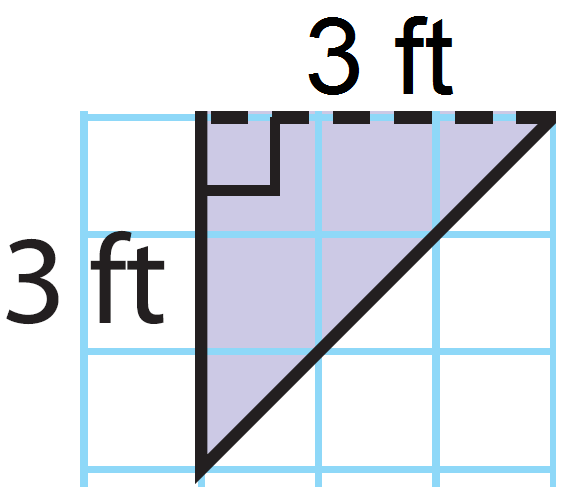
Base (b) = 3 ft

Height (h) = 3 ft

Use the formula.

A = (1/2)bh

= (1/2)(3)(3)

= 4.5

The area of the second triangle is 4.5 square ft.

Step 5 :

Add the areas to find the total area.

A = 3 + 44 + 4.5

= 51.5

So, the area of the given composite figure is 51.5 square feet.

Problem 3 :

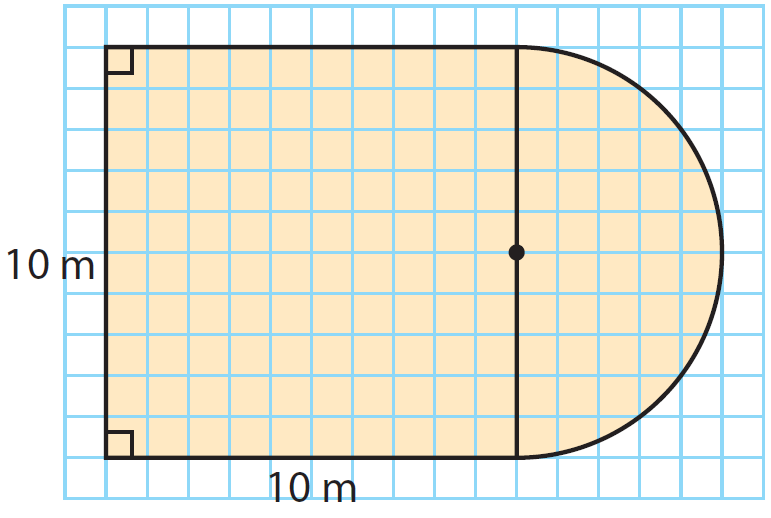
Find the area of the figure given below.

Solution :

Step 1 :

Separate the figure into smaller, familiar figures: a square and a semicircle.

Step 2 :

Find the area the square.

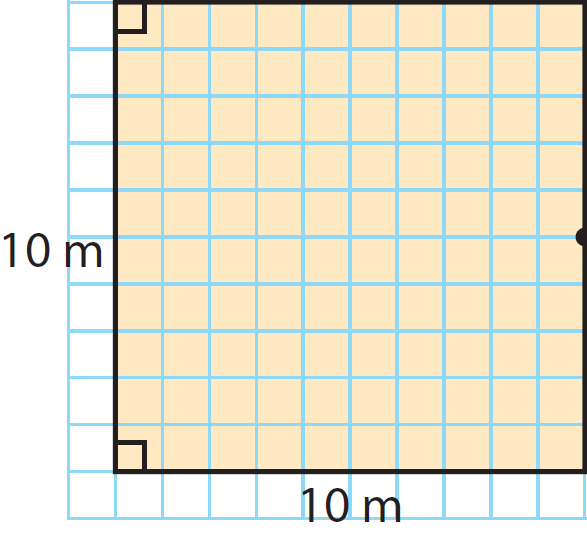
Length of each side = 10 m

Use the formula.

A = Side x Side

= 10 x 10

= 100

The area of the rectangle is 100 square meter.

Step 3 :

Find the area the semicircle.

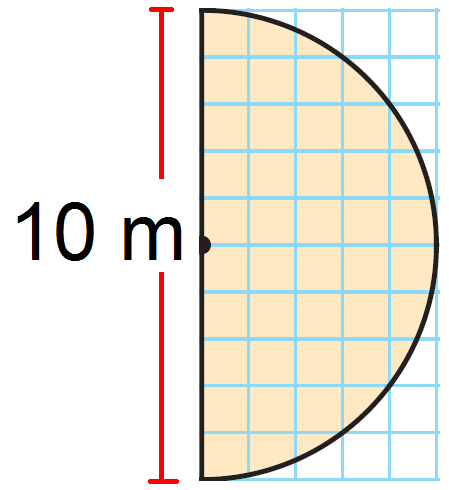
Diameter = 10 m

Radius (r) = Diameter/2

= 10/2

= 5 m

Use the formula.

A = (1/2)πr²

= (1/2)(3.14)(5)²

= 1.57 x 25

= 39.25

The area of the semi circle is about 39.25 square meter.

Step 4 :

Add the areas to find the total area.

A = 100 + 39.25

= 139.25

So, the area of the given composite figure is about 139.25 square meter.

Problem 4 :

Luis is going to paint a basketball court on his driveway, as shown in the diagram below. This basketball court consists of a rectangle and a semicircle.

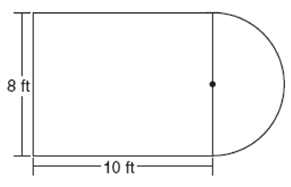
Which expression represents the area of this basketball court, in square feet?

1) 80      2) 80 + 8π        3) 80 + 16π      4) 80 + 64π

Solution :

Area of rectangle = length x width

Area if semicircle = (1/2) πr²

length = 10 ft, width = 8 ft and radius = 4 ft

= 10 x 8 + (1/2) π(4)²

= 80 + (1/2) π(16)

= 80 + 8π

So, option 2) is correct.

Problem 5 :

A figure is made up of a rectangle and a semicircle as shown in the diagram below.

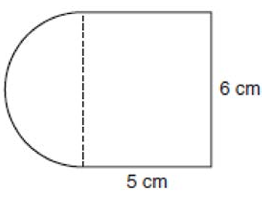
What is the area of the figure, to the nearest tenth of a square centimeter?

1) 39.4     2) 48.8      3) 44.1      4) 58.3

Solution :

Area of figure = area of rectangle + area of semicircle

length = 5 cm, width = 6 cm and radius = 3 cm

= 5 x 6 + (1/2) π(3)²

= 30 + 3.14 x 4.5

= 30 + 14.13

= 44.13 cm²

Problem 6 :

In the diagram below, circle O is inscribed in square ABCD. The square has an area of 36.

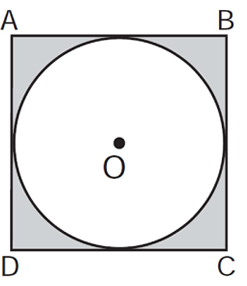
What is the area of the circle?

1) 9π      2) 6π      3) 3π       4) 36π

Solution :

Area of square = 36 square units

Let x be the side length of the square.

x² = 36

x = √36

x = 6 units

Diameter of the circle = 6 units

Radius of the circle = 3 units

Area of circle = πr²

= π(3²)

= 9π

So, option 1) is correct.

Problem 7 :

A patio consisting of two semicircles and a square is shown in the diagram below. The length of each side of the square region is represented by 2x.

Write an expression for the area of the entire patio, in terms of x and π .

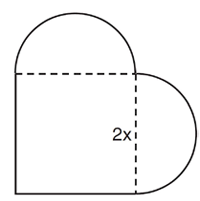
Solution :

Total area = area of square + 2 x area of semicircle

= 2x(2x) + 2(1/2) πr²

= 4x² + πx²

= x² (4 + π) square units

Problem 8 :

A designer created the logo shown below. The logo consists of a square and four quarter-circles of equal size.

Express, in terms of π, the exact area, in square inches, of the shaded region.

= Area of square - 4(area of quadrant)

Side length of square = 6 inches

Radius of quadrant = 3 inches

= 6² - 4(1/4) πr²

= 36 - 3.14(3²)

= 36 - 3.14(9)

= 36 - 28.26

= 7.74 square inches

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.