FINDING THE AREA OF A CIRCLE USING A PARALLELOGRAM

In this section, you will learn how to find area of a circle using parallelogram through the following steps.

Step 1 : 

Use a compass to draw a circle and cut it out.

Step 2 : 

Fold the circle three times as shown to get equal wedges.

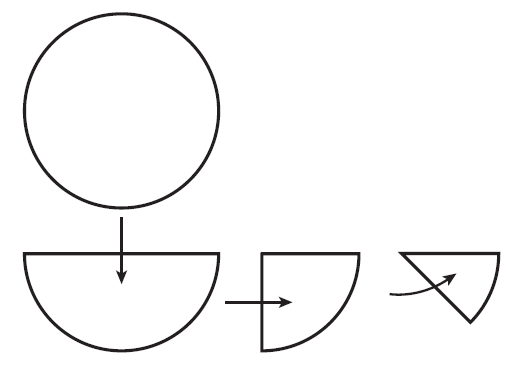
Step 3 : 

Unfold and shade one-half of the circle.

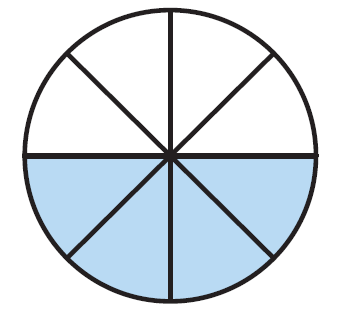
Step 4 : 

Cut out the wedges, and fit the pieces together to form a figure that looks like a parallelogram.

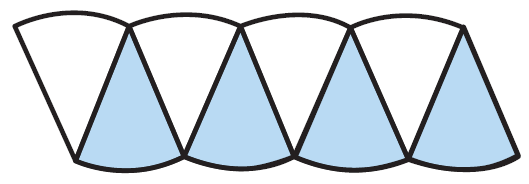
The base and height of the parallelogram relate to the parts of the circle.

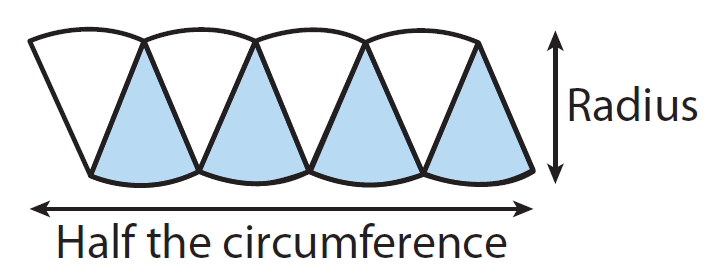
Base b  =  Half of the circumference of the circle. 

or b  =  πr

Height h  =  radius of the circle

or h  =  r

We know that the formula to find area of the parallelogram is

A  =  bh 

To find the area of the circle, substitute πr for b and r for h in the above area formula.

A  =   πr x r

A  =   πr²

Hence, the formula to find area of a circle is πr² square units. 

Reflect : 

How can we make the wedges look more like a parallelogram ?

Make the wedges smaller so the base looks more like a straight line than curves. 

Finding Area of a Circle - Examples

Example 1 :

Find the area of a circle whose radius is 7 cm.

Solution :

Step 1 : 

Area of a circle  =  πr²

Radius is given in the question. That is 7 cm. 

Substitute r  =  7  in the above formula. 

Area of the circle  =  π(7)²

Step 2 :

Since radius is a multiple of 7, we can use π  ≈  22/7.

Area of the circle  ≈  (22/7) x (7)²

Simplify

Area of the circle  ≈  22 x 7

Area of the circle  ≈  154 square cm. 

So, the area of the circle is about 154 square cm.

Example 2 :

Find the area of a circle whose diameter is 40 inches.

Solution :

Step 1 : 

Area of a circle  =  πr²

We know that

Radius  =  Diameter / 2

Radius  =  40/2  =  20 inches 

Step 2 :

Substitute r  =  20  in the above formula. 

Area of the circle  =  π(20)²

Step 3 :

Since radius is not a multiple of 7, we can use π  ≈  3.14.

Area of the circle  ≈  (3.14) x (20)²

Area of the circle  ≈  3.14 x 400

Area of the circle  ≈  1256 square in. 

So, the area of the circle is about 1256 square in.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.