FINDING THE AREA AND CIRCUMFERENCE OF A CIRCLE

Area : 

Area of a circle is defined as the space occupied by the circular object on a flat surface. The area of a shape can be measured by comparing the shape to squares of a fixed size. 

Circumference :

The perimeter of a circle is called its circumference. In other words, the distance around the edge of a circle.

Formulas for Circumference and Area of a Circle

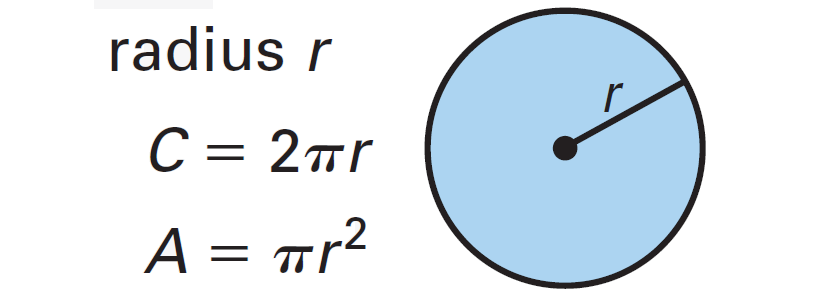
The measurements of perimeter use units such as centimeters, meters, kilometers, inches, feet, yards, and miles. The measurements of area use units such as square centimeters (cm²), square meters(m²), and so on.

Example 1 :

An irrigation sprinkler waters a circular region with a radius of 14 feet. Find the circumference of the region watered by the sprinkler.  Use 22/7 for π.

Solution : 

Use the formula. 

C  =  2πr

Substitute 14 for r. 

C  =  2π(14)

Substitute 22/7 for π. 

C  ≈  2 x (22/7) x 14

Simplify 

C  ≈  2 x (22/1) x 2

C  ≈  88

So, the circumference of the region watered by the sprinkler is about 88 feet.

Example 2 :

The diameter of a car wheel is 21 inches. Find the circumference of the wheel. 

Solution : 

Radius  =  Diameter / 2 

Radius  =  21/2 inches

Use the formula. 

C  =  2πr

Substitute 21/2 for r. 

C  =  2π(21/2)

Substitute 22/7 for π. 

C  ≈  2 x (22/7) x (21/2)

Simplify.

C  ≈  2 x (11/1) x (3/1)

C  ≈  66

So, the circumference of the wheel is 66 inches. 

Example 3 :

Find the diameter, radius, circumference and area of the circle shown below. use 3.14 as an approximation for π.

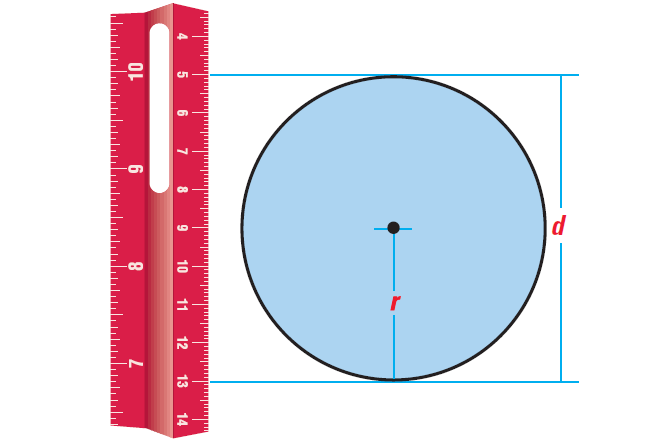
Solution :

From the diagram shown above, we can see that the diameter of the circle is 

d  =  13 - 5  =  8 cm

The radius is one half the diameter. So, the radius is

r  =  d/2  =  8/2  =  4 cm

Using the formula for circumference, we have

C  =  2πr  ≈  2(3.14)4

C  ≈  25.1 cm

Using the formulas for area, we have

A  =  πr²  ≈  (3.14)(4)²

A  ≈  50.24 square cm.

Example 4 :

A biscuit recipe calls for the dough to be rolled out and circles to be cut from the dough. The biscuit cutter has a radius of 4 cm. Find the area of the top of the biscuit once it is cut. Use 3.14 for π.

Answer :

Since the top of the biscuit is in the shape of a circle, we can use area of circle formula to find area of the top of the biscuit.   

Step 1 : 

Area of a circle  =  πr²

Radius is given in the question. That is 4 cm. 

Substitute 4 for r in the above formula. 

Area of the circle  =  π(4)²

Step 3 :

Since radius is not a multiple of 7, we can use π  ≈  3.14.

Area of the circle  ≈  (3.14) x (4)²

Area of the circle  ≈  3.14 x 16

Area of the circle  ≈  50.24 square cm. 

The area of the biscuit is about 50.24 square cm.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.