FINDING SQUARE ROOT BY PRIME FACTORIZATION METHOD
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
The following steps will be useful to find square root of a number by prime factorization.
(i) Decompose the number inside the square root into prime factors.
(ii) Inside the square root, for every two same numbers multiplied, one number can be taken out of the square root.
(iii) Combine the like square root terms using mathematical operations.
Example :
√3 - √12 + √27 = √3 + - √(2 ⋅ 2 ⋅ 3) + √(3 ⋅ 3 ⋅ 3)
= √3 - 2√3 + 3√3
= 2√3
Practice Questions
Find the square root each of the following numbers prime factorization.
Question 1 :
36
Answer :
Decompose 36 into prime factors using synthetic division.
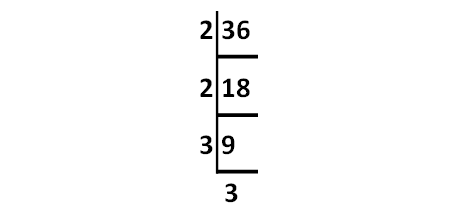
√36 = √(2 ⋅ 2 ⋅ 3 ⋅ 3)
= (2 ⋅ 3)
= 6
Question 2 :
144
Answer :
Decompose 144 into prime factors using synthetic division.

√144 = √(2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 3 ⋅ 3)
= (2 ⋅ 2 ⋅ 3)
= 12
Question 3 :
256
Answer :
Decompose 256 into prime factors using synthetic division.
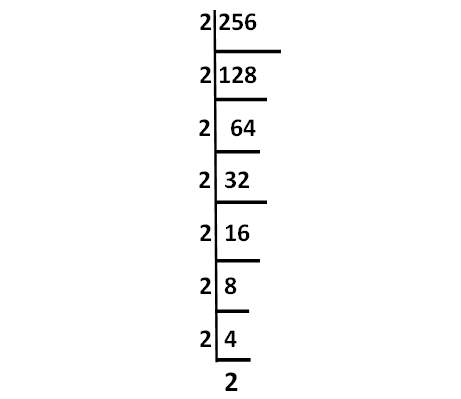
√256 = √(2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2)
= (2 ⋅ 2 ⋅ 2 ⋅ 2)
= 16
Question 4 :
324
Answer :
Decompose 324 into prime factors using synthetic division.

√324 = √(2 ⋅ 2 ⋅ 3 ⋅ 3 ⋅ 3 ⋅ 3)
= 2 ⋅ 3 ⋅ 3
= 18
Question 5 :
400
Answer :
Decompose 400 into prime factors using synthetic division.
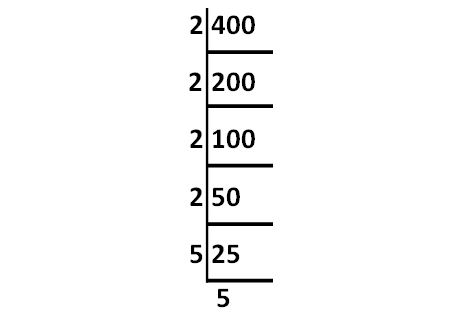
√400 = √(2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 5 ⋅ 5)
= (2 ⋅ 2 ⋅ 5)
= 20
Question 6 :
625
Answer :
Decompose 625 into prime factors using synthetic division.
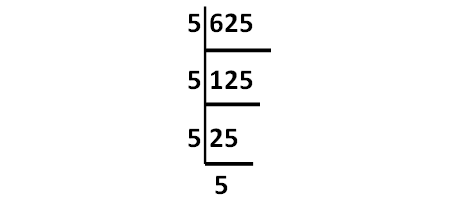
√625 = √(5 ⋅ 5 ⋅ 5 ⋅ 5)
= 5 ⋅ 5
= 25
Question 7 :
1024
Answer :
Decompose 1024 into prime factors using synthetic division.
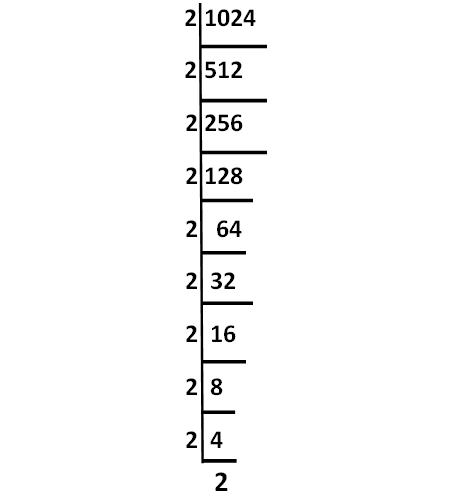
√1024 = √(2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2)
= (2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2)
= 32
Question 8 :
2025
Answer :
Decompose 2025 into prime factors using synthetic division.

√2025 = √(5 ⋅ 5 ⋅ 3 ⋅ 3 ⋅ 3 ⋅ 3)
= (5 ⋅ 3 ⋅ 3)
= 45
Question 9 :
3136
Answer :
Decompose 3136 into prime factors using synthetic division.

√3136 = √(2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 7 ⋅ 7)
= (2 ⋅ 2 ⋅ 2 ⋅ 7)
= 56
Question 10 :
4096
Answer :
Decompose 4096 into prime factors using synthetic division.
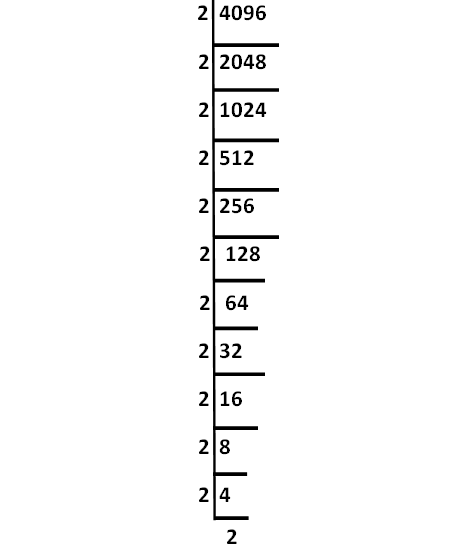
√4096 = √(2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2)
= (2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2)
= 64
Question 11 :
√8 + √125
Answer :
|
√8 = √(2 ⋅ 2 ⋅ 2) √8 = 2 |
√125 = √(5 ⋅ 5 ⋅ 5) √125 = 5 |
√8 + √125 = 2 + 5
= 7
Question 12 :
(√34)(√136)
Answer :
(√34)(√136) = √(34 ⋅ 136)
= √(2 ⋅ 17 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 17)
= 2 ⋅ 2 ⋅ 17
= 68
Question 13 :
(14√117) ÷ (7√52)
Answer :
Decompose 117 and 52 into prime factors using synthetic division.
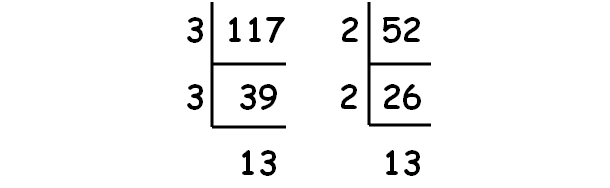
|
√117 = √(3 ⋅ 3 ⋅ 13) √117 = 3√13 |
√52 = √(2 ⋅ 2 ⋅ 13) √52 = 2√13 |
(14√117) ÷ (7√52) :
= 14(3√13) ÷ 7(2√13)
= 42√13 ÷ 14√13
= 42√13/14√13
= 3
Question 14 :
(4√7)2
Answer :
(4√7)2 = 4√7 ⋅ 4√7
= (4 ⋅ 4)(√7 ⋅ √7)
= (16)(7)
= 112
Question 15 :
(√5)3(√125)
Answer :
(√5)3 + √125 = (√5 ⋅ √5 ⋅ √5)√(5 ⋅ 5 ⋅ 5)
= (5√5)(5√5)
= (5 ⋅ 5)(√5 ⋅ √5)
= (25)(5)
= 125
Question 16 :
√(0.361 / 0.00169) = ?
a) 1.9/1.3 b) 19/13 c) 19/130 d) 190/13
Answer :
= √(0.361 / 0.00169)
0.361 = 0.361 x (1000/1000)
= 361/1000
Since we have 3 digits after the decimal, we have to multiply and divide by 1000.
0.00169 = 0.00169 x (100000/100000)
= 169/100000
√(0.361 / 0.00169) = √(361/1000) / (169/100000)
= √(361/1000) x (100000/169)
= √(361 x 100)/169
= √(19 x 19 x 10 x 10)/(13 x 13)
= (19 x 10) / 13
= 190/13
So, option d is correct.
Question 17 :
(√24 + √216)/√96 = ?
a) 2√6 b) 2 c) 6√2 d) 2/√6
Answer :
= (√24 + √216)/√96
√24 = √(2 x 2 x 2 x 3)
= 2√6
√216 = √(2 x 2 x 2 x 3 x 3 x 3)
= 2 x 3√(2 x 3)
= 6√6
√96 = √2 x 2 x 2 x 2 x 2 x 3
= 2 x 2√(2 x 3)
= 4√6
(√24 + √216)/√96 = (2√6 + 6√6)/4