FINDING SLOPE AND Y INTERCEPT FROM A GRAPH WORKSHEET

Problem 1 :

Find the slope and y-intercept from the graph shown below.

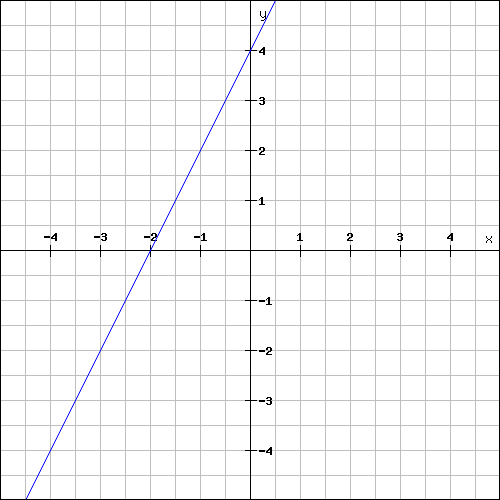
Problem 2 :

Find the slope and y-intercept from the graph shown below.

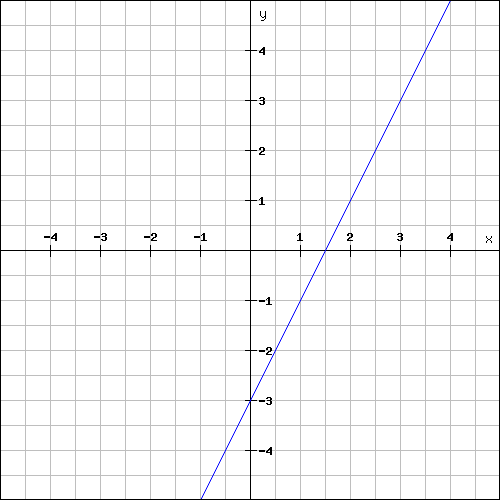
Problem 3 :

Find the slope and y-intercept from the graph shown below.

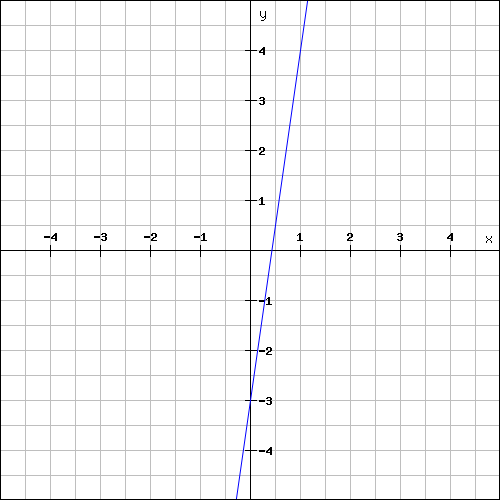
Solutions

Problem 1 :

Find the slope and y-intercept from the graph shown below.

Solution :

y-intercept :

The y-intercept of the line is the value of y at where the line intersects the y-axis.

The above line intersects the y-axis at 4.

So, 

y-intercept  =  4

Slope :

The above line is a rising line.

So, its slope will be a positive value.

Plot the two points (-2, 0) and (0, 4) on the line and measure the rise and run. 

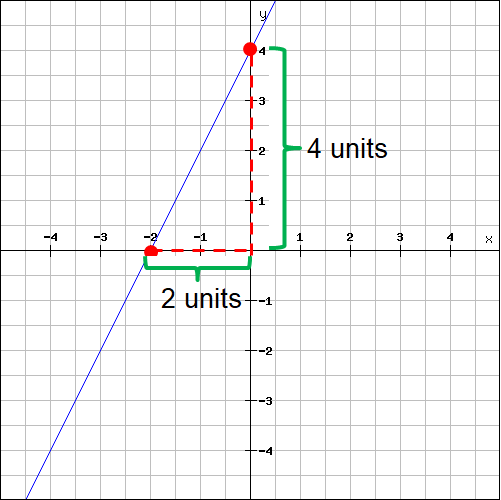
For the above line, 

Rise  =  4

Run  =  2

Then, slope is 

m  =  rise / run

m  =  4/2

m  =  2

Alternative Method : 

Formula to find slope is

m  =  (y₂ - y₁) / (x₂ - x₁)

Substitute (x₁, y₁)  =  (-2, 0) and (x₂, y₂)  =  (0, 4) 

m  =  (4 - 0) / (0 + 2)

m  =  4/2

m  =  2

Problem 2 :

Find the slope and y-intercept of a linear function from the graph given below.

Solution :

y-intercept :

The y-intercept of the line is the value at where the line intersects the y-axis.

The above line intersects the y-axis at -3.

So,

y-intercept  =  -3

Slope :

The above line is a rising line line.

So, its slope will be a positive value.

Plot the two points (1, -1) and (2, 1) on the line and measure the rise and run. 

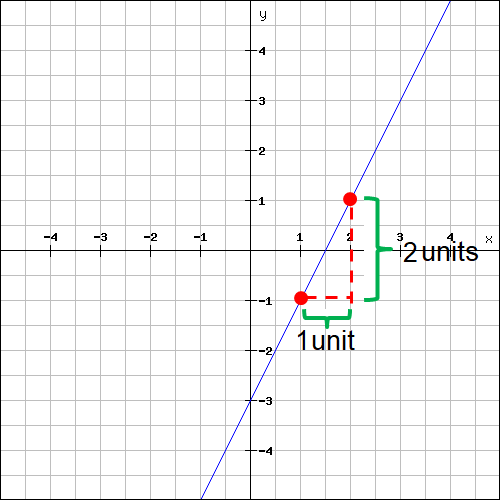
For the above line, 

Rise  =  2

Run  =  1

Then, slope is 

m  =  rise / run

m  =  2/1

m  =  2

Alternative Method : 

Formula to find slope is

m  =  (y₂ - y₁) / (x₂ - x₁)

Substitute (x₁, y₁)  =  (1, -1) and (x₂, y₂)  =  (2, 1) 

m  =  (1 + 1) / (2 - 1)

m  =  2/1

m  =  2

Problem 3 :

Find the slope and y-intercept of a linear function from the graph given below.

Solution :

y-intercept :

The y-intercept of the line is the value at where the line intersects the y-axis.

The above line intersects the y-axis at -3.

So,

y-intercept  =  -3

Slope :

The above line is a rising line line.

So, its slope will be a positive value.

Plot the two points (0, -3) and (1, 4) on the line and measure the rise and run. 

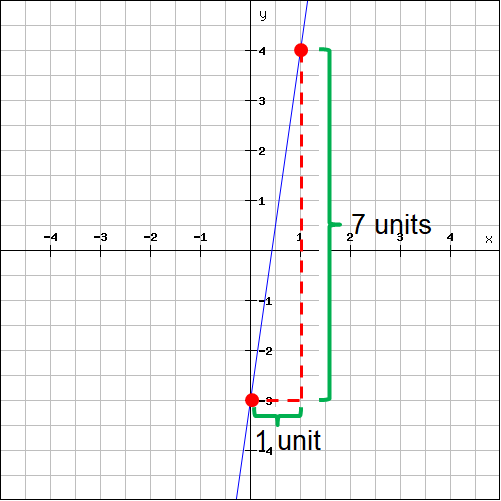
For the above line, 

Rise  =  7

Run  =  1

Then, slope is 

m  =  rise / run

m  =  7/1

m  =  7

Alternative Method : 

Formula to find slope is

m  =  (y₂ - y₁) / (x₂ - x₁)

Substitute (x₁, y₁)  =  (0, -3) and (x₂, y₂)  =  (1, 4) 

m  =  (4 + 3) / (1 - 0)

m  =  7/0

m  =  7

Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here. 

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.