FINDING RATIOS FROM TABLES

Ratio is a comparison of two quantities with same kind. In this section, we are going to see, how to find ratios from the tables. 

Example :

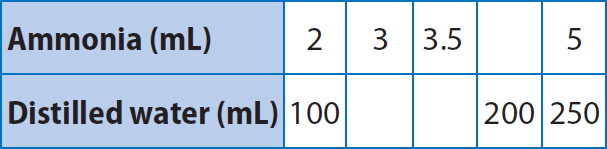
Students in Mr. Webster’s science classes are doing an experiment that requires 250 milliliters of distilled water for every 5 milliliters of ammonia. The table shows the amount of distilled water needed for various amounts of ammonia.

Question 1 : 

Use the numbers in the first column of the table to write a ratio of distilled water to ammonia.

Solution :

100 ml distilled water / 2 ml ammonia  (or)  100 : 2

Question 2 : 

How much distilled water is used for 1 milliliter of ammonia?

Solution :

From the first column of the table, the ratio  of distilled water to ammonia is 

100 ml water / 2 ml ammonia

To find the quantity of distilled water used for 1 milliliter of ammonia, we have to make the second quantity (ammonia) as 1. 

100 ml distilled water : 2 ml ammonia  =  (100 ÷ 2) / (2 ÷ 2)

100 ml distilled water : 2 ml ammonia  =  50 / 1

That is,

50 ml distilled water / 1 ml ammonia  

The quantity of distilled water used for 1 milliliter of ammonia is 50 ml.

Question 3 : 

Use your answer from question 2, write another ratio of distilled water to ammonia.

Solution :

To write another ratio from the answer of question 2, we have find an equivalent ratio to 50 : 1.

To find equivalent ratio of the given ratio, we have to multiply both the terms of the ratio by the same non zero number, say "2".

Then, we have 

(50x2) : (1x2)  =  100 : 2

Therefore, another ratio of distilled water to ammonia is 100 : 2

Question 4 : 

Check whether the two ratios from answers of question 1 and question 2 are equivalent or not equivalent. 

Solution :

The two ratios from the answers of question 1 and 2 are 

100 : 2 and 50 : 1 

Let us check, whether two rations 100 : 2 and 50 : 1 are equivalent or not equivalent. 

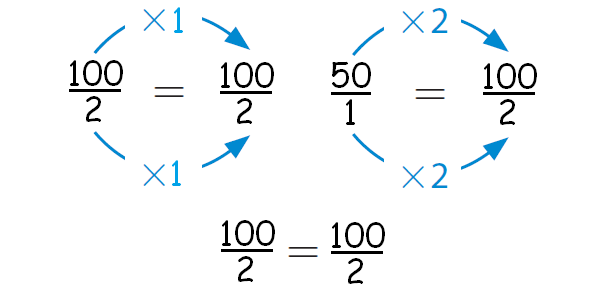
From the above working, it is clear that the two ratios 100 : 2 and 50 : 1 are equivalent.

Question 5 :

Complete the table. What are the equivalent ratios shown in the table ?

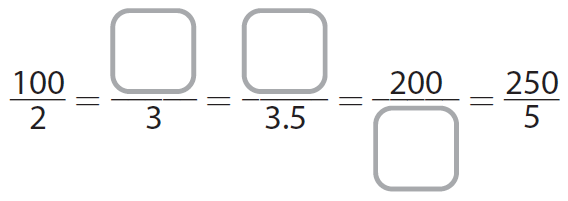
Solution :

For the first blank :

(100 ÷ 2) / (2 ÷ 2)  =  50 / 1

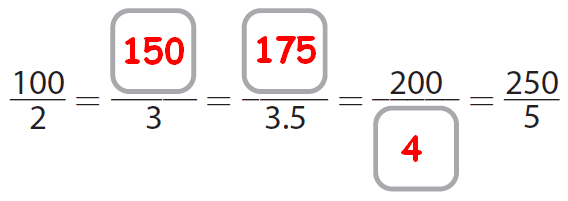
(50 x 3) / (1 x 3)  =  150 / 3

For the second blank :

(100 ÷ 2) / (2 ÷ 2)  =  50 / 1  

(50 ÷ 2) / (1 ÷ 2)  =  25 / 0.5

(25 x 7) / (0.5 x 7)  =  175 / 3.5

For the third blank :

(100 x 2) / (2 x 2)  =  200 / 4

Then, we have

Question 6 :

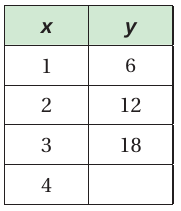
Using the numbers from the table, find and state the rule in words. Then find the missing value.

Solution :

Let x be the input and y be the output.

Ratio between input and output is 1 : 6

Let y be the missing output.

1 : 6 = 4 : y

1/6 = 4/y

y = 4(6)

y = 24

So, the missing output is 24.

Question 7 :

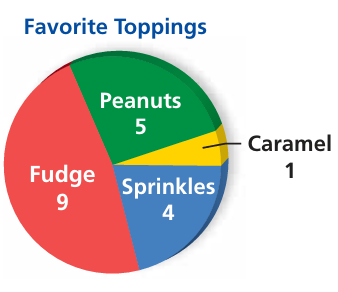
The circle graph shows the favorite ice-cream toppings of several students. Use ratio language to compare the number of students who favor peanuts to the total number of students.

Solution :

Total number of students = 5 + 1 + 4 + 9

= 19

Number of students who prefer peanuts = 5

Ratio between peanuts to total number of students.

= 5 : 19

Question 8 :

Lightning strikes Earth 1000 times in 10 seconds. How many times does lightning strike per second?

Solution :

Number of lightning strikes = 1000

Time taken = 10 seconds

Number of lightning strike per second = 1000/10

= 100 strikes

Question 9 :

You jog 2 kilometers in 12 minutes. At this rate, how long will it take you to complete a 5-kilometer race?

Solution :

Distance covered = 2 kilometers

Time taken = 12 minutes

Let x be the time taken to cover 5 kilometers.

2 : 12 = 5 : x

2/12 = 5/x

2x = 5(12)

x = 5(6)

x = 30

To jog 5 kilometers it takes 30 minutes.

Question 10 :

A printer prints 28 photos in 8 minutes.

a. How many minutes does it take to print 21 more photos?

b. How many minutes does it take to print 35 more photos?

Solution :

a)  28 photos in 8 minutes

Let x be the number of minutes for taking 21 photos.

28 : 8 = 21 : x

28/8 = 21/x

28x = 21(8)

x = 21(8)/28

x = 6 minutes

b) Let x be the number of minutes for taking 35 photos.

28 : 8 = 35 : x

28/8 = 35/x

28x = 35(8)

x = 35(8)/28

x = 10 minutes

Question 11 :

You mix 8 tablespoons of hot sauce and 3 cups of salsa in a green bowl. You mix 12 tablespoons of hot sauce and 4 cups of salsa in an orange bowl. Which mixture is hotter?

Solution :

Ratio between hot sauce to cups of salsa in a green bowl

= 8 : 3

Ratio between hot sauce to cups of salsa in a orange bowl

= 12 : 4

= 3 : 1

Multiplying both parts by 3, we get

= 9 : 3

Orange bowl mixture is hotter.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.