FINDING RATE OF CHANGE FROM A WORD PROBLEM

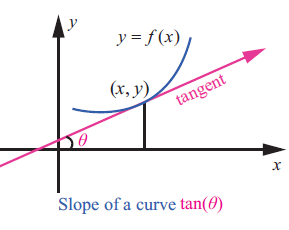
If θ is the angle made by the tangent to the curve

y  =  f(x)

at the point (x, y) , then the slope of the curve at (x, y) is f'(x) = tanθ,

where θ is measured in the anti clock wise direction from the X -axis. Note that, f ′(x) is also denoted by

dy/dx 

and also called instantaneous rate of change.

Problem 1 :

If the volume of a cube of side length x is v = x³ . Find the rate of change of the volume with respect to x when x = 5 units.

Solution :

v  =  x³

dv/dx  =  3x²

dv/dx at x  = 5  ==>  3(5)²

=  75 units.

Problem 2 :

If the mass m(x) (in kilograms) of a thin rod of length x (in meters) is given by, m(x) = √3x then what is the rate of change of mass with respect to the length when it is x = 3 and x = 27 meters.

Solution :

m(x) = √3√x

Rate of change of mass  m'(x)  =  √3(1/2√x)

m'(x)  =  (√3/2√x)

When x  =  3

m'(3)  =  (√3/2√3)  ==>  1/2 kg/m

When x  =  27

m'(27)  =  (√3/2√27)  ==>  1/6 kg/m

Problem 3 :

A stone is dropped into a pond causing ripples in the form of concentric circles. The radius r of the outer ripple is increasing at a constant rate at 2 cm per second. When the radius is 5 cm find the rate of changing of the total area of the disturbed water?

Solution :

Area of ripple(A)  =  πr²

dr/dt  =  2 cm/sec

r  =  5

Supposed to find dA/dt

dA/dt  =  2πr (dr/dt)

dA/dt  =  2π(5)(2)

dA/dt  =  20π

Problem 4 :

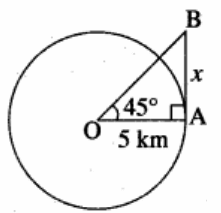
A beacon makes one revolution every 10 seconds. It is located on a ship which is anchored 5 km from a straight shore line. How fast is the beam moving along the shore line when it makes an angle of 45° with the shore?

Solution :

Rate of revolution by the beacon :

1 revolution  =  10 seconds

360 degree  =  10 seconds

1 sec  =  2π/10

Angular velocity (d θ/dt)  =  2π/10  ==>  π/5

In the triangle,

tan θ  =  Opposite side/ Adjacent side

differentiating x  =  5 tan θ

dx/dt  =  5 sec²θ (dθ/dt)

dx/dt  =  5 sec²45 (π/5)

dx/dt  =  5 (√2)² (π/5)

dx/dt  =  2π km/sec

So, the beam is moving at the rate of 2π km/sec.

Problem 5 :

If a ball is thrown into the air with a velocity of 40 ft/s, its height in feet after t seconds is given by

y = -16t² + 40t

a) Find the average velocity for the time period beginning when t = 2 lasting 0.5 s 

b) Find the instantaneous velocity when t = 2.

Solution :

y = -16t² + 40t

Average velocity = f(x₂) - f(x₁) / (x₂ - x₁)

= f(2.5) - f(2) / (2.5 - 2)

f(2.5) = -16(2.5)² + 40(2.5)

= -100 + 100

0

f(2) = -16(2)² + 40(2)

= -16(4) + 80

= -64 + 80

= 16

(2.5, 0) ( 2, 16)

Average velocity = (16 - 0)/(2 - 2.5)

= 16/-0.5

= 32

b) Instantaneous rate of change at x = 2

dy/dt = -16(2t) + 40(1)

= -32t + 40

= -32(2) + 40

= -64 + 40

= -24

Problem 6 :

If an arrow is shot upward on the moon with a velocity of 58 m/s, its height in meters after t seconds is given by:

h = 58t - 0.83t²

a) Find the velocity of the arrow at 1 s.

b) Find the velocity of the arrow when t=a.

c) When will the arrow hit the moon?

d) With what velocity will the arrow hit the moon?

Solution :

a)  h = 58t - 0.83t²

Rate of change of height = velocity

= 58(1) - 0.83 (2t)

h'(t) = 58 - 1.66t

When t = 1

h'(1) = 58 - 1.66(1)

= 58 - 1.66

= 56.34

b) Velocity at t = a

h'(a) = 58 - 1.66a

c)  When the height is 0, at the that time the arrow will hit the moon.

0 = 58t - 0.83t²

t(58 - 0.83t) = 0

t = 0 and 0.83t = 58

t = 58/0.83

t = 69.8

After 69.8 seconds the 

d) h'(t) = 58 - 1.66t

Velocity = h'(t) = 58 - 1.66t

h'(69.8) = 58 - 1.66(69.8)

= 58 - 115.868

= -57.868 m/s

Problem 7 :

Temperature readings (in degrees C) where recorded every hour starting at 5:00 am on a day in April in Whitefish, Montana. This table shows some of the readings:

Find the rate of average rate of change for each change in time:

a) 8:00 am to 11:00 am

b) 8:00 am to 10:00 am

c) 8:00 am to 9:00 am

Solution :

a) (8, 6.1) and (11, 12.1)

Average rate of change = (12.1 - 6.1) / (11 - 8)

= 6/3

= 2

b) (8, 6.1) and (10, 10)

Average rate of change = (10 - 6.1) / (10 - 8)

= 3.9/2

= 1.95

c) (8, 6.1) and (9, 8.3)

Average rate of change = (8.3 - 6.1)/(9 - 8)

= 2.2/1

= 2.2

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.