FINDING RATE OF CHANGE FROM A GRAPH

Example 1 :

The graph shows the distance Nathan bicycled over time. What is Nathan’s rate of change ?

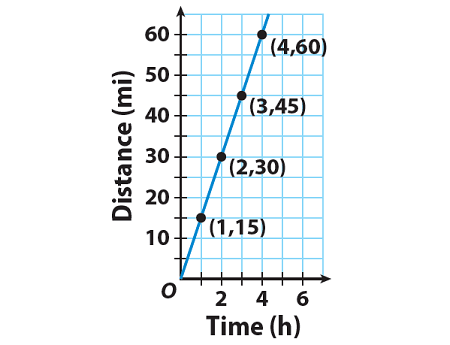
Solution :

Step 1 :

Identify the independent and dependent variables.

Independent : Time

Dependent : Distance

Step 2 :

Find the rates of change. 

0 hour to 1 hour :

Change in distance/Change in time  =  (15 - 0)/(1 - 0) 

Change in distance/Change in time  =  15/1 

Change in distance / Change in time  =  15 

1 hours to 4 hours :

Change in distance/Change in time  =  (60 - 15)/(4 - 1) 

Change in distance/Change in time  =  45/3 

Change in distance/Change in time  =  15 

2 hours to 4 hours :

Change in distance/Change in time  =  (60 - 30)/(4 - 2) 

Change in distance/Change in time  =  30/2 

Change in distance/Change in time  =  15 

Nathan’s rate of change is 15 miles per hour. 

Reflect : 

1.  Recall that the graph of a proportional relationship is a line through the origin. Explain whether the relationship between Nathan’s time and distance is a proportional relationship.

Yes ; the graph is a line through the origin.

2.  Does it matter what interval you use when you find the rate of change of a proportional relationship ? Explain.

No ; in a proportional relationship, the rate of change is constant.

Example 2 :

The graph shows the rate at which water is leaking from a tank. Find the rate at which the water is leaking from the tank per minute. 

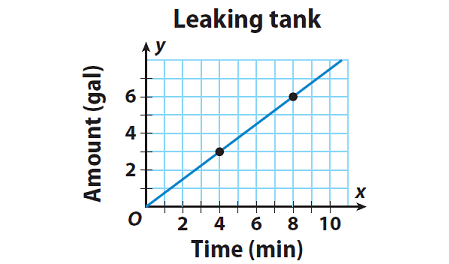
Solution :

Step 1 :

Identify the independent and dependent variables.

Independent : Time

Dependent : Leakage

Step 2 :

Find the rates of change. 

0 hours to 4 hours :

Leakage/Change in time  =  (3 - 0)/(4 - 0)

Leakage/Change in time  =  3/4 

Leakage/Change in time  =  0.75 

4 hours to 8 hours :

Leakage/Change in time  =  (6 - 3)/(8 - 4) 

Leakage/Change in time  =  3/4 

Leakage/Change in time  =  0.75 

1 hour to 8 hours :

Leakage/Change in time  =  (6 - 0)/(8 - 0) 

Leakage/Change in time  =  6/8 

Leakage/Change in time  =  3/4 

Leakage/Change in time  =  0.75 

The water is leaking at the rate of 0.75 gallons per minute.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.