FINDING QUOTIENT AND REMAINDER USING LONG DIVISION
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Question 1 :
Find the quotient and remainder of the following.
(i) (4x3 + 6x2 – 23x +18) ÷ (x + 3)
Solution :
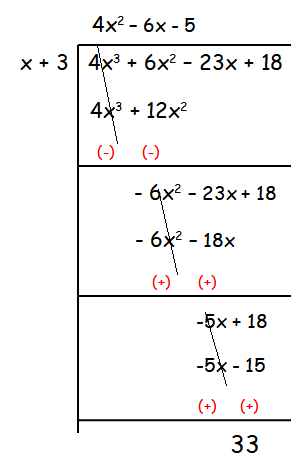
Quotient = 4x2 - 6x - 5
Remainder = 33
(ii) (8y3 – 16y2 + 16y –15) ÷ (2y – 1)
Solution :
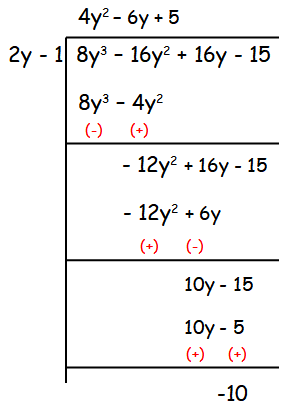
Quotient = 4y2 - 6y + 5
Remainder = -10
(iii) (8x3 – 1) ÷ (2x – 1)
Solution :
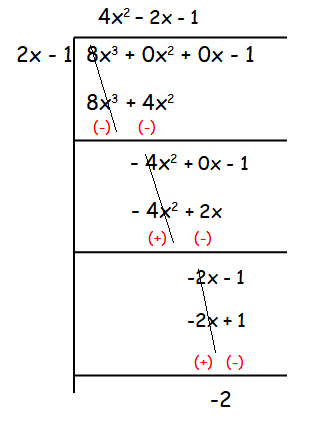
Quotient = 4x2 - 2x - 1
Remainder = -2
(iv) (-18z + 14z2 + 24z3 + 18) ÷ (3z + 4)
Solution :
= (-18z + 14z2 + 24z3 + 18) ÷ (3z + 4)
Arrange the given polynomial according to the power.
= (24z3 + 14z2 -18z + 18) ÷ (3z + 4)

Quotient = 8z2 - 6z + 2
Remainder = 10
Question 2 :
The area of a rectangle is x2 + 7x + 12. If its breadth is (x + 3), then find its length
Solution :
Area of rectangle = length x breadth
x2 + 7x + 12 = length (x + 3)
Length = (x2 + 7x + 12) / (x + 3)
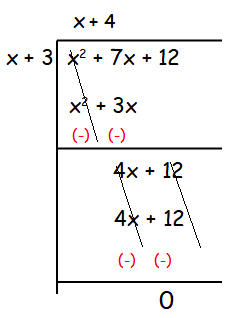
Hence x + 4 is the breadth of the rectangle.
Question 3 :
The base of a parallelogram is (5x + 4). Find its height, if the area is 25x2 – 16.
Solution :
Area of parallelogram = base x height
base = 5x + 4
Area = 25x2 - 16
25x2 - 16 = (5x + 4) ⋅ height
Height = (25x2 - 16) / (5x + 4)
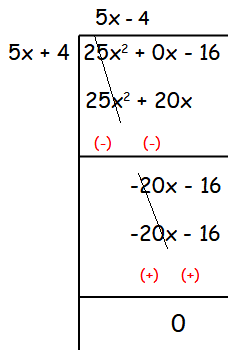
Hence height of the given parallelogram is 5x - 4.
Question 4 :
The sum of (x + 5) observations is (x3 + 125). Find the mean of the observations.
Solution :
Sum of (x + 5) observation = x3 + 125
Total number of observation = x + 5
Mean observation = (x3 + 125)/(x + 5)
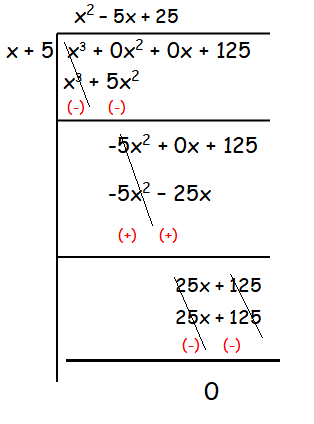
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
10 Hard SAT Math Questions (Part - 44)
Jan 12, 26 06:35 AM
10 Hard SAT Math Questions (Part - 44) -
US Common Core K-12 Curricum Algebra Solving Simple Equations
Jan 07, 26 01:53 PM
US Common Core K-12 Curricum Algebra Solving Simple Equations -
10 Hard SAT Math Questions (Part - 4)
Jan 05, 26 06:56 PM
10 Hard SAT Math Questions (Part - 4)
