FINDING QUADRATIC FUNCTIONS WORKSHEET

Problem 1 :

Find the quadratic function in vertex form, if the vertex is (2, 3). and its graph is passing through the point (5, 21).

Problem 2 :

Find the quadratic function in standard form, if the vertex is (-1, -2). and its graph is passing through the point (0, 4).

Problem 3 :

Find the quadratic function in standard form, if the two x-intercepts are 2 and 5 and its graph is passing through the point (1, 3).

Problem 4 :

Find the quadratic function in standard form, if the vrtex is (5, 7) and its graph is passing through the point (-1, 0).

Problem 5 :

Find the quadratic function in vertex form, if the maximum point is (2, 5) and x-intercept is 1.

Problem 6 :

Find the quadratic function in vertex form, if the axis of symmetry is x = 5, range yis and y-intercept is 

Answers

1. Answer :

Quadratic function in vertex form :

y = a(x - h)² + k

Here (h, k) is the vertex.

Given : Vertex is (2, 3).

Substitute (h, k) = (2, 3).

y = a(x - 2)² + 3

Given : Graph is passing through the point (5, 21).

Substitute x = 5 and y = 21.

21 = a(5 - 2)² + 3

21 = a(3)² + 3

21 = 9a + 3

Subtract 3 from both sides.

18 = 9a

Divide both sides by 9.

2 = a

The required quadratic function in vertex form :

y = 2(x - 2)² + 3

2. Answer :

Quadratic function in vertex form :

y = a(x - h)² + k

Here (h, k) is the vertex.

Given : Vertex is (-1, -2).

Substitute (h, k) = (-1, -2).

y = a[x - (-1)]² + (-2)

y = a(x + 1)² - 2

Given : Graph is passing through the point (0, 4).

Substitute x = 0 and y = 4.

4 = a(0 + 1)² - 2

4 = a(1)² - 2

4 = a - 2

Add 2 to both sides.

6 = a

The required quadratic function in vertex form :

y = 6(x + 1)² - 2

3. Answer :

Quadratic function in standard form :

y = ax² + bx + c

If the x = p and y = q are two x-intercepts, then the quadratic function is

y = a(x - p)(x - q)

Since x = 2 and x = 5 are two x-intercepts, the quadratic function is

y = a(x - 2)(x - 5)

Given : Graph is passing through the point (1, 8).

Substitute x = 1 and y = 8.

8 = a(1 - 2)(1 - 5)

8 = a(-1)(-4)

8 = 4a

Divide both sies by 4.

2 = a

The required quadratic function in standard form :

y = 2(x - 2)(x - 5)

y = 2(x² - 5x - 2x + 10)

y = 2(x² - 7x + 10)

y = 2x² - 14x + 20

4. Answer :

Since the vertex is given, initially we can write the quadratic function in vertex form and convert it to standard form.

Quadratic function in vertex form :

y = a(x - h)² + k

Given : Vertex is (5, 7).

Substitute (h, k) = (5, 7).

y = a(x - 5)² + 7

Given : Graph is passing through the point (4, 0).

Substitute x = 4 and y = 0.

0 = a(4 - 5)² + 7

0 = a(-1)² + 7

0 = a(1) + 7

0 = a + 7

Subtract 7 from both sides.

-7 = a

The required quadratic function in vertex form :

y = -7(x - 5)² + 7

Convert it to standard form.

y = -7(x² - 10x + 25) + 7

y = -7x² + 70x - 175 + 7

y = -7x² + 70x - 168

5. Answer :

The graph of a quadratic function is a parabola.

Sketch a parabola with the maximum point (2, 5) and x-intercept (1, 0).

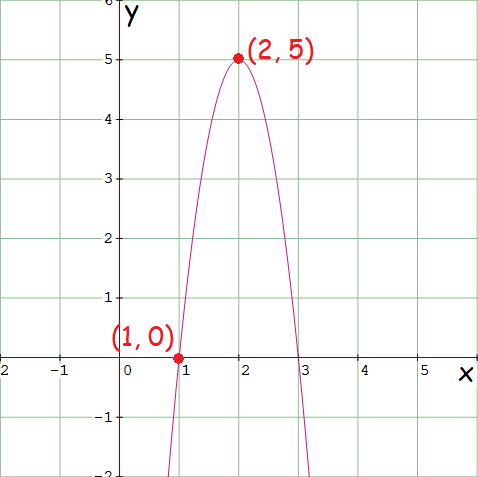
The vertex of the parabola above is (2, 5).

Quadratic function in vertex form :

y = a(x - h)² + k

Substitute (h, k) = (2, 5).

y = a(x - 2)² + 5

Since the x-intercept is (1, 0), substitute x = 1 and y = 0 to find the value of a.

0 = a(1 - 2)² + 5

0 = a(-1)² + 5

0 = a(1) + 5

0 = a + 5

-5 = a

The required quadratic function in vertex form :

y = -5(x - 2)² + 5

6. Answer :

Sketch a parabola for the following  :

Axis of symmetry : x = 5

Range : y ≥ 2

y-intercept : (0, 7)

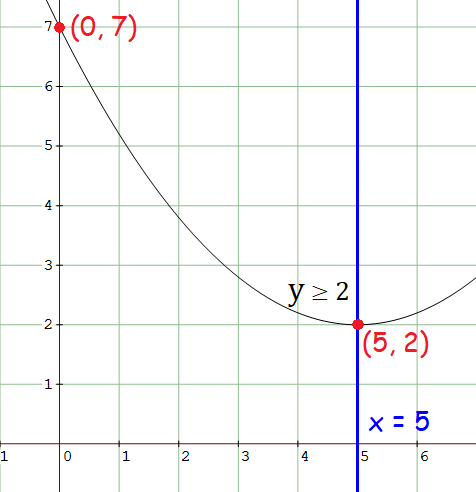
The vertex of the parabola above is (5, 2).

Quadratic function in vertex form :

y = a(x - h)² + k

Substitute (h, k) = (5, 2).

y = a(x - 5)² + 2

Since the y-intercept is (0, 7), substitute x = 0 and y = 7 to find the value of a.

7 = a(0 - 5)² + 2

7 = a(-5)² + 2

7 = 25a + 2

5 = 25a

⅕ = a

The required quadratic function in vertex form :

Convert it to standard form.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.