FINDING MISSING MEASURES IN SIMILAR TRIANGLES

Because corresponding angles are congruent and corresponding sides are proportional in similar triangles, we can use similar triangles to solve real-world problems.

Example 1 :

While playing tennis, David is 12 meters from the net, which is 0.9 meter high. He needs to hit the ball so that it just clears the net and lands 6 meters beyond the base of the net. At what height should Matt hit the tennis ball ?

Solution :

Step 1 :

Draw an appropriate diagram to the given information.

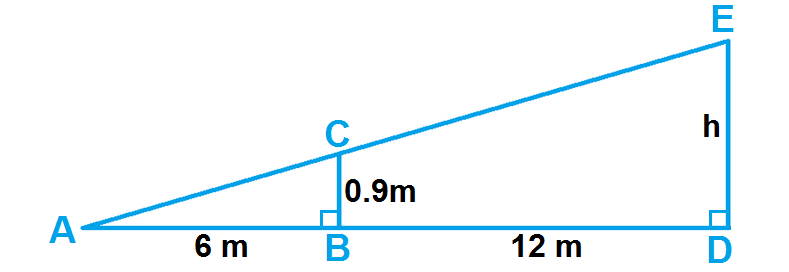
In the above diagram,

BC = Height of the net

DE = Height of ball when hit

A = Point at where the ball lands

Step 2 :

Let us compare two corresponding angles of triangle ABC and ADE.

Because two angles in one triangle are congruent to two angles in the other triangle, the two triangles are similar.

Step 3 :

Since the triangle ABC and ADE are similar triangles,  corresponding side lengths are proportional.

AD/AB = DE/BC

(AB + BD)/AB = DE/BC

Substitute the lengths from the figure.

(6 + 12)/6 = h/0.9

18/6 = h/0.9

3 = h/0.9

Multiply both sides by 0.9

3 ⋅ 0.9 = (h/0.9) ⋅ 9

2.7 = h

So, David should hit the ball at a height of 2.7 meters.

Example 2 :

Jose is building a wheelchair ramp that is 24 feet long and 2 feet high. She needs to install a vertical support piece 8 feet from the end of the ramp. What is the length of the support piece in inches ?

Solution :

Step 1 :

Draw an appropriate diagram to the given information.

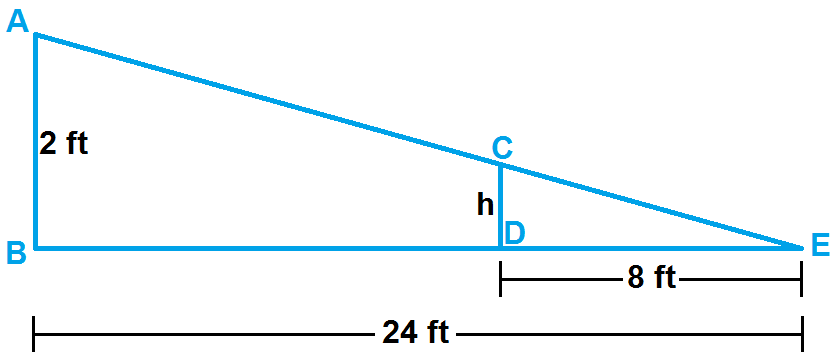
In the above diagram,

AB = Height of the chair

CD = Height of the support piece

E = End of the ramp

Step 2 :

Let us compare two corresponding angles of triangle ABE and CDE.

Because two angles in one triangle are congruent to two angles in the other triangle, the two triangles are similar.

Step 3 :

Since the triangle ABE and ADE are similar triangles,  corresponding side lengths are proportional.

So, we have

DE/BE = CD/AB

Substitute the lengths from the figure.

8/24 = h/2

1/3 = h/2

Multiply both sides by 2.

(1/3) ⋅ 2 = (h/2) ⋅ 2

2/3 = h

or

h = 2/3 ft

Step 4 :

Convert feet into inches.

Since 1 ft = 12 inches, we have to multiply by 12 to convert ft to inches.

h = (2/3) ⋅ 12 inches

h = 8 inches

So, the length of the support piece is 8 inches.

Example 3 :

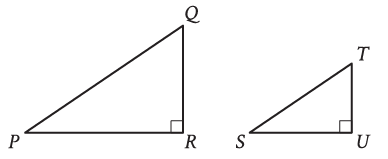
Right traingles PQR and STU are similar, where P corresponds to S. IF the measure of angle Q is 18 degree what is the measure of angle S ?

a)  18     b)  72     c)  82     d) 162

Solution :

In triangle PQR,

∠P + ∠Q + ∠R = 180

∠Q = 18 and ∠R = 90

∠P + 18 + 90 = 180

∠P + 108 = 180

∠P = 180 - 108

∠P = 72

Since ∠P and ∠S are corresponding angles, ∠S = 72. Option b is correct.

Example 4 :

The cheerleaders at City High make their own megaphones by cutting off the small end of a cone made from heavy paper. If the small end of the megaphone is to have a radius of 2.5 cm, what should be the height of the cone that is cut off?

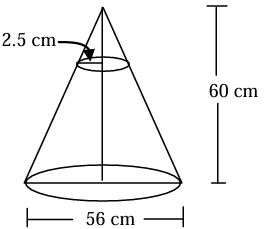
Solution :

We see two triangles,

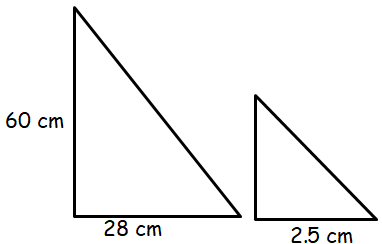
Let h be the height of the small triangle.

Comparing corresponding sides,

60/28 = h/2.5

Doing cross multiplication, we get

h = 60(2.5)/28

h = 5.35 cm

So, height of teh cone to be cut is 5.35 cm.

Example 5 :

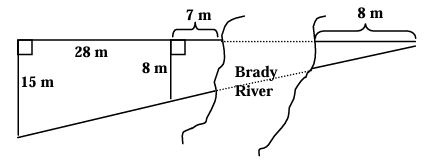
Find the width of the Brady River.

Solution :

We observe two right triangles,

Let x be the width of brady river.

height of the large triangle 28 + 7 + x + 8

= 43 + x

base of larger triangle = 15 m

base of smaller triangle = 8 m

(43 + x)/15 = (15 + x)/8

8(43 + x) = 15(15 + x)

344 + 8x = 225 + 15x

15x - 8x = 344 - 225

7x = 119

x = 119/7

x = 17

So, the width of the river is 17 m.

Example 6 :

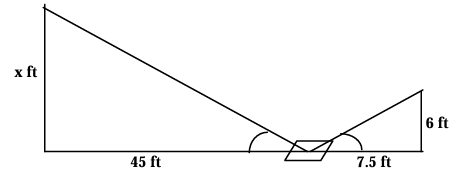
Ramon places a mirror on the ground 45 ft from the base of a geyser. He walks backward until he can see the top of the geyser in the middle of the mirror. At that point, Ramon’s eyes are 6 ft above the ground and he is 7.5 ft from the mirror. Use similar triangles to find the height of the geyser.

Solution :

Comparing the corresponding sides,

x/45 = 6/7.5

x = 6(45)/7.5

x = 36 ft

So, the missing height is 36 ft.

Example 7 :

Find the height of the giraffe in the diagram below.

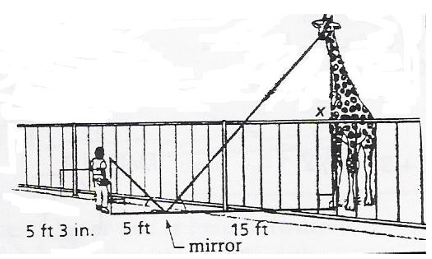
1 ft = 12 inches

5 ft = 5(12) ==> 60 inches

5 ft 3 in = 60 + 3 ==> 63 inches

Compairng the corresponding sides,

63/5 = x/15

x = 63(15)/5

x = 63(3)

x = 189 ft

15 x 12 = 180

x = 180 inches + 9 inches

x = 15 ft 9 in

So, the height is 15 ft 9 in

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.