FINDING MISSING ANGLES IN TRAINGLES WORKSHEET

Find the missing angle in a the triangles given below.

(1)

(2)

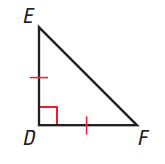
(3)

(4)

(5)

(6)

(7)

(8)

(9)

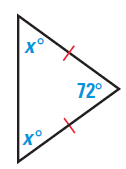
(10)

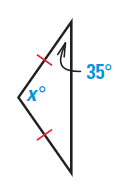
11)  In a triangle ABC, ∠ A = 2X+7, ∠ B = 5X-15, and ∠ C = 6X. What is the value of x and what are the measures of angles A, B, and C?

12)  In a triangle XYZ, ∠ X = 67°, ∠ Y = 47°, and ∠ Z = 3x + 6. What is the value of x and what is the measure of ∠Z?

13)  Two angles of a triangle have equal measures, but the third angle's measure is 36° less than the sum of the other two. Find the measure of each angle of the triangle.

14)  Find the measures of the angles of an isosceles triangle if the measure of the vertex angle is 40 degrees less than the sum of the measures of the base angles.

Problem 1 :

Solution :

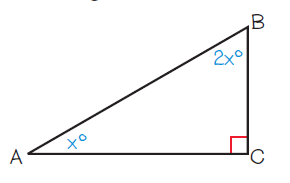
<A+<B+<C  =  180

Given <A  =  x, <B  =  2x and <C  =  90

x+2x+90  =  180

3x+90  =  180

3x  =  180-90

3x  =  90

x  =  90/3

x  =  30

So, <A  =  30 and <B  =  60.

Problem 2 :

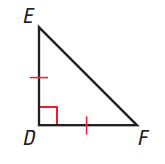
<D + <E + F  =  180  ----(1)

Since it is isosceles triangle, <E  =  <F and <D  =  90

Let <E  =  x

90 + x + x  =  180

2x+90  =  180

Subtracting 90 on both sides, we get

2x  =  90

Divide by 2 on both sides, we get

x  =  90/2

x  =  45

Problem 3 :

Solution :

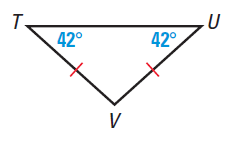
<T  =  42, <U  =  42, <V  =  ?

<U + <V + <T  =  180

42 + <V + 42  =  180

<V + 84  =  180

Subtracting by 84 on both sides, we get

<V  =  96

Problem 4 :

Solution :

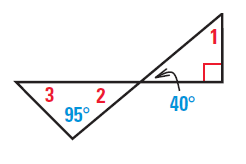
Vertically opposite angles are equal. So <2  =  40.

<1 + 40 + 90  =  180

<1 + 130  =  180

<1  =  50

<3 + <2 + 95  =  180

<3+40  =  180

<3  =  140

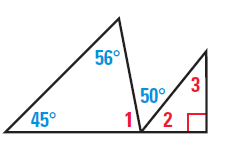
Problem 5 :

Solution :

In small triangle the indicated angle is 90 degree.

Using exterior angle theorem,

56+45  =  50 + <2

<2  =  101-50

<2  =  51

<1 + <2 + 50  =  180

<1+51+50  =  180

<1+101 =  180

<1  =  180-101

<1  =  79

In small triangle,

<2+<3+90  =  180

51 + <3 + 90  =  180

<3  =  180-141

<3  =  39

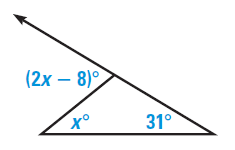
Problem 6 :

Solution :

By using exterior angle theorem,

x+31  =  2x-8

2x - x  = 31 + 8

x  =  39

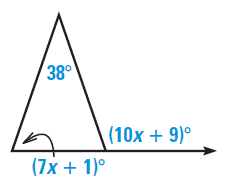
Problem 7 :

Solution :

Using exterior angle theorem,

10x+9  =  7x+1+38

10x-7x  =  39 - 9

3x  =  30

x  =  10

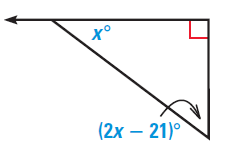
Question 8 :

Solution :

Sum of interior angles of a triangle

x + 2x-21 + 90  =  180

3x+69  =  180

Subtracting 69 on both sides, we get

3x  =  180-69

3x  =  111

Dividing by 3 on both sides, we get

x  =  111/3

x  =  37

Question 9 :

Solution :

Sum of interior angle of triangle  =  180

x+x+72  =  180

Subtracting 72 on both sides

2x  =  180-72

2x  =  108

Dividing by 2 on both sides

x  =  54

Question 10 :

Solution :

Since it is isosceles triangle, the angle formed by equal sides will be equal.

x+35+35  =  180

x+70  =  180

Subtracting 70 on both sides

x  =  180-70

x  =  110

Problem 11 :

In triangle ABC,

Given that ∠ A = 2X - 4 , ∠ B = 5X + 15, and ∠ C = 6X

Solution :

Sum of interior angles of triangle = 180 degree

∠A + ∠B + ∠C = 180

2X - 4 + 5X + 15 + 6X = 180

Combining the like terms, we get

2X + 5X + 6X + 11 = 180

13X = 180 - 11

13X = 169

X = 169/13

X = 13

So, angles ∠A, ∠B and ∠C are 22, 80 and 78 respectively.

Problem 12 :

In a triangle XYZ, ∠X = 67°, ∠Y = 47°, and ∠Z = 3x + 6.

Solution :

Sum of interior angles of triangle = 180 degree

∠X + ∠Y + ∠Z = 180

67 + 47 + 3x + 6 = 180

Combining the like terms, we get

120 + 3x = 180

3x = 180 - 120

3x = 60

x = 60/3

x = 20

Applying the value of x, 

∠Z = 3(20) + 6

= 60 + 6

∠Z = 66

Problem 13 :

Two angles of a triangle have equal measures, but the third angle's measure is 36° less than the sum of the other two. Find the measure of each angle of the triangle.

Solution :

Let x be the two angles which are having equal measures.

Since the third measure is 36 less than the sum of the other two, third angle measure will be x - 36

x + x + x - 36 = 180

3x = 180 + 36

3x = 216

x = 216/3

x = 72

Third angle = 72 - 36 ==> 36

So, the three angle measures are 72, 72 and 36 respectively.

Problem 14 :

Find the measures of the angles of an isosceles triangle if the measure of the vertex angle is 40 degrees less than the sum of the measures of the base angles.

Solution :

Since the given triangle is isosceles, two angle measures will be equal.

Let the measure of equal angles be x, sum of these two angles = x + x ==> 2x

Vertex angle = 2x - 40

Sum of interior angles = 180

2x + 2x - 40 = 180

4x = 180 + 40

4x = 220

x = 220/4

= 55

So, the equal measures are 55 and 55.

Vertex angle = 2(55) - 40

= 110 - 40

= 70

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.