FINDING MEASUREMENTS OF A TRIANGLE

Example 1 :

Find the area and perimeter of the triangle shown below. 

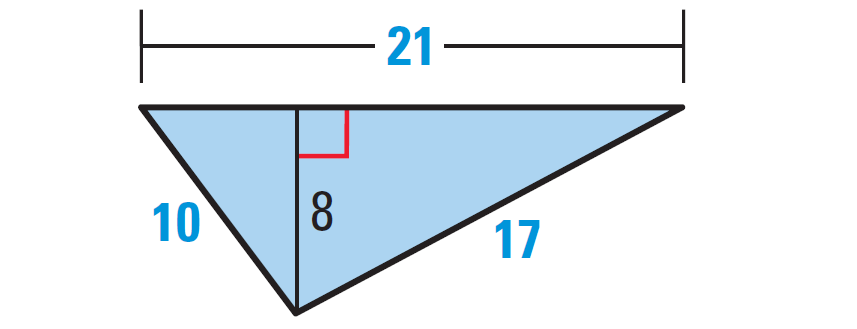
Solution : 

Because we want to find the area of the triangle, we have to know its base and height. 

To know the base and height of the triangle, let us rotate the given triangle as shown below. 

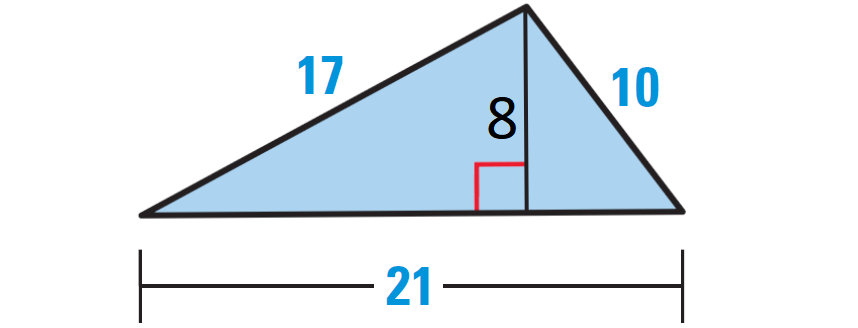
Base = 21 units and height = 8 units. 

Area of the triangle :

=  (1/2)⋅ base ⋅ height

 =  (1/2) ⋅ 21 ⋅ 8

=  84 square units

Perimeter of the triangle :

=  Sum of the lengths of all the three sides

=  17 + 10 + 21

=  48 units 

Example 2 :

Find the area and perimeter of the triangle given below. 

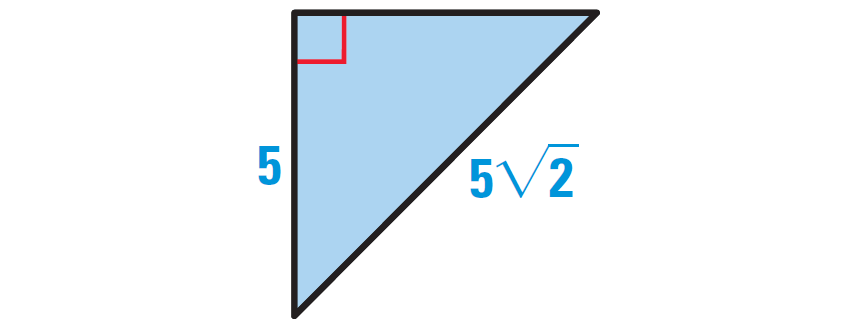
Solution : 

Because we want to find the area of the triangle, we have to know its base and height. 

To know the base and height of the triangle, let us rotate the given triangle as shown below. 

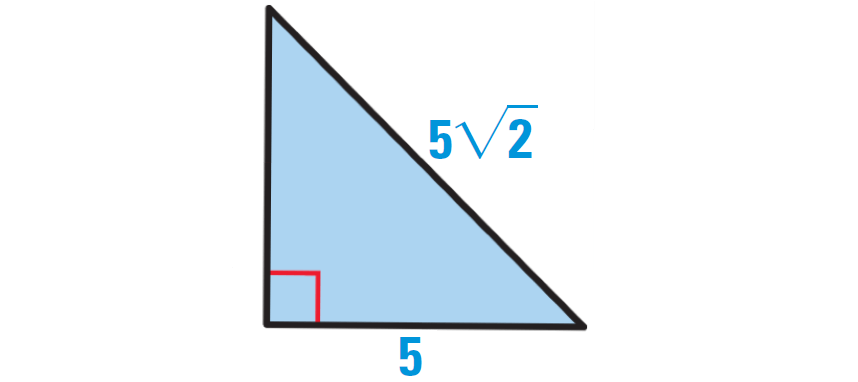
Use Pythagorean theorem to find the height of the triangle.

h² + 5²  =  (5√2)²

h² + 25  =  5² ⋅ (√2)²

h² + 25  =  25 ⋅ 2

h² + 25  =  50

Subtract 25 from each side. 

h²  =  25

h²  =  5²

h  =  5

Area of the triangle : 

=  (1/2) ⋅ base ⋅ height

=  (1/2) ⋅ 5 ⋅ 5

=  12.5 square units

Perimeter of the triangle :

=  Sum of the lengths of all the three sides

=  5 + 5 + 5√2

=  (10 + 5√2) units

Example 3 :

Area of the triangle shown below is 126 square units. Find the perimeter and height of the triangle. 

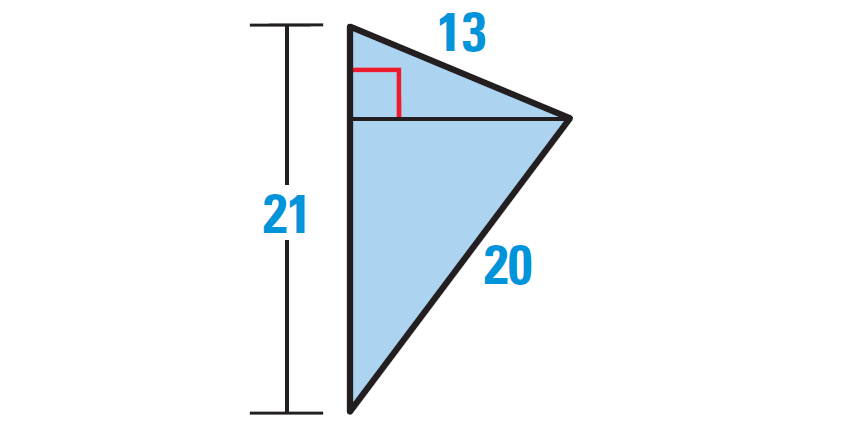
For our convenience, let us rotate the given triangle as shown below. 

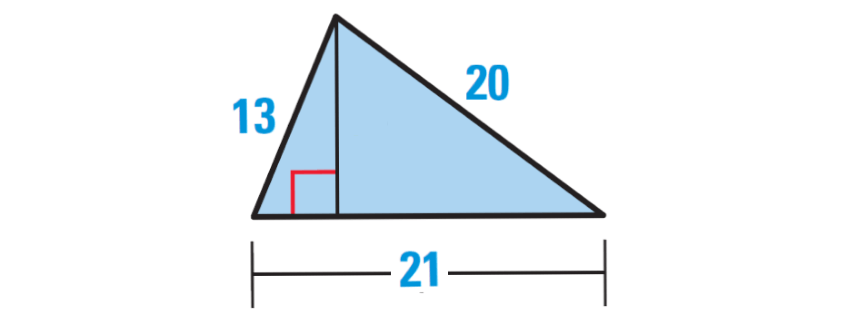
In the triangle above, base = 21 units.

Given :

Area of the triangle  =  126 square units

(1/2) ⋅ base ⋅ height  =  126

Substitute base = 21.

(1/2) ⋅ 21 ⋅ height  =  126

Multiply each side by 2.

21 ⋅ height  =  126⋅2

21 ⋅ height  =  252

Divide each side by 21.

(21 ⋅ height)/21  =  252/21

height  =  12

Perimeter of the triangle : 

=  Sum of the lengths of all the three sides

=  13 + 20 + 21

=  54 units

Example 4 :

Find the area and perimeter of the triangle defined by D(1, 3), E(8, 3) and F(4, 7). 

Solution : 

Plot the points in the coordinate plane. Draw the height from F to the side DE. Label the point where the height meets DE as G. Point G has coordinates (4, 3). 

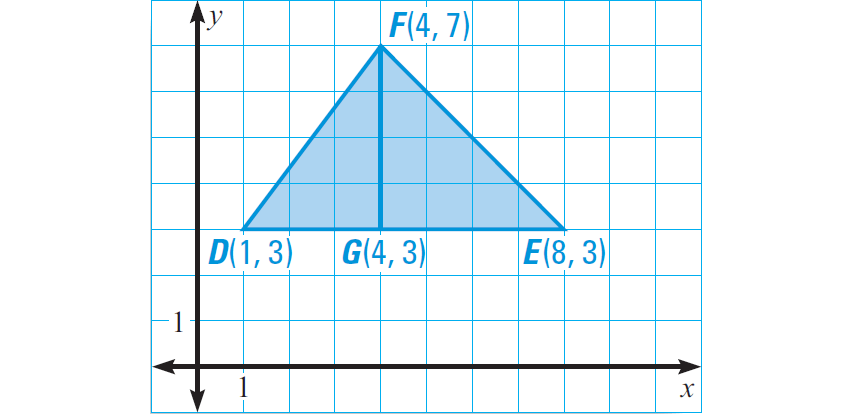
Length of DE : 

=  8 - 1

=  7

Use distance formula to find the length of EF and FD.

Distance Formula :

=  √[(x₂ - x₁)² + (y₂ - y₁)²]

Length of EF : 

(x₁, y₁)  =  E(8, 3)

(x₂, y₂)  =  F(4, 7)

EF  =  √[(4 - 8)² + (7 - 3)²]

EF  =  √[(-4)² + (4)²]

EF  =  √[16 + 16]

EF  =  √32

EF  =  √(4 ⋅ 4 ⋅ 2)

EF  =  4√2

Length of FD : 

(x₁, y₁)  =  F(4, 7)

(x₂, y₂)  =  D(1, 3)

FD  =  √[(1 - 4)² + (3 - 7)²]

FD  =  √[(-3)² + (-4)²]

FD  =  √[9 + 16]

FD  =  √25

FD  =  5

Perimeter of the triangle :

=  5 + 7 + 4√2

=  (12 + 4√2) units

Example 5 :

Shown is an equilateral triangle with side length of 8cm. Six of the triangles are put together to make a larger shape. Find the perimeter of the larger shape.

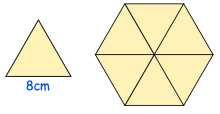
Solution :

The larger shape is hexagon, it consists of 6 equal sides with the measure of 8 cm.

Perimeter = 6(8) + 6(8)

= 48 + 48

= 96 cm

So, the perimeter of the larger shape is 96 cm.

Example 6 :

An isosceles triangle has a perimeter of 73 cm An equilateral triangle has a perimeter of 51 cm The triangles are put together to make a kite.

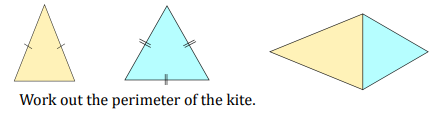
Solution :

Perimeter of isosceles triangle = 73 cm

Perimeter of equilateral triangle = 51 cm

Let side length of equilateral triangle be x.

3x = 51

x = 51/3

x = 17

Perimeter of kite = perimeter of isosceles triangle + 2(17)

= 73 + 34

= 107 cm

Example 7 :

The triangle and square have the same perimeter. Find x

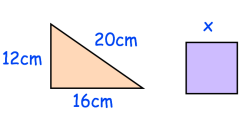
Solution :

Perimeter of triangle = 16 + 12 + 20

= 48 cm

Perimeter of square = 4x

4x = 48

x = 48/4

x = 12 cm

So, the value of x is 12 cm.

Find the perimeter of an equilateral triangle of side 9 cm

Example 8 :

Find the perimeter of an isosceles triangle whose equal sides are 8 cm each and third side is of 6 cm.

Solution :

Perimeter of isosceles triangle = sum of length of all sides

= 8 + 8 + 6

= 16 + 6

= 22 cm

Example 9 :

Two sides of a triangle are 12 cm and 14 cm. If the perimeter of the triangle is 36 cm, find the third side .

Solution :

Two sides of the triangle are 12 cm and 14 cm.

Perimeter of triangle = 36 cm

Let x be the length of third side.

12 + 14 + x = 36

x = 36 - 26

x = 10

So, the length of the third side is 10 cm.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.