FINDING MAXIMUM AND MINIMUM VALUE OF QUADRATIC FUNCTION

The vertex of a parabola is the point where the line of symmetry of the parabola intersects the parabola.

Let f be a quadratic function with standard form

y  =  a(x - h)² + k

the maximum and minimum value of f occurs at x  =  h.

In order to find the maximum or minimum value of quadratic function, we have to convert the given quadratic equation in the above form.

Minimum Value of Parabola :

If the parabola is open upward, then it will have minimum value

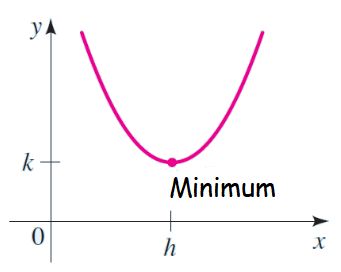
If a > 0, then minimum value of f is f(h)  =  k

Maximum Value of Parabola :

If the parabola is open downward, then it will have maximum value.

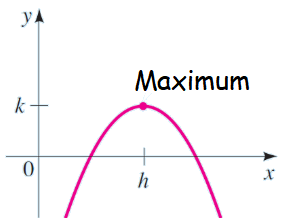
If a < 0, then maximum value of f is f(h)  =  k

Finding Maximum or Minimum Value of a Quadratic Function

Question 1 :

Suppose f , g, and h are defined by

f(x) = −x², g(x) = −2x², h(x) = −2x² + 1.

(a) Sketch the graphs of f , g, and h on the interval [−1, 1].

(b) Find the vertex of the graph of f , the graph of g, and the graph of h.

(d) What is the maximum value of f ? The maximum value of g? The maximum value of h?

Solution :

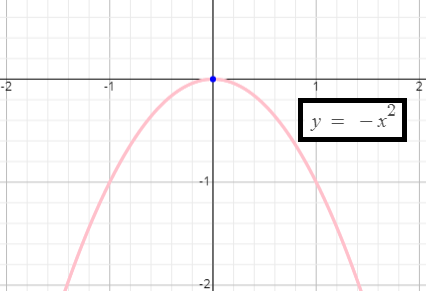
Graph of f(x) = −x² :

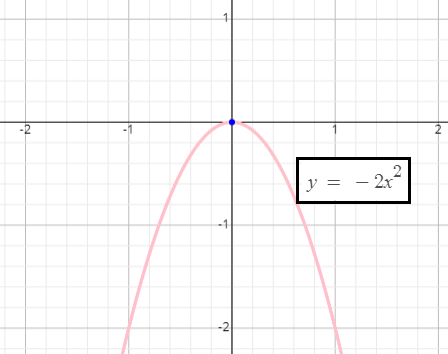
Graph of f(x) = −2x² :

Graph of f(x) = −2x² + 1 

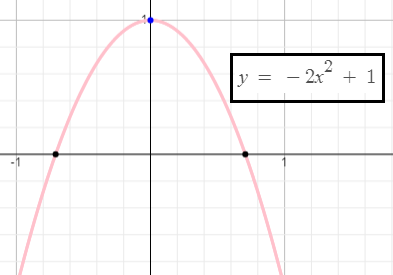
(b)  The vertex of the parabola f(x) = −x² is at (0, 0). Hence the maximum value is 0.

The vertex of the parabola f(x) = −2x² is at (0, 0). Hence the maximum value is 0.

The vertex of the parabola f(x) = −2x² + 1 is at (0, 1). Hence the maximum value is 1.

Question 2 :

The function defined by 

f(x) = x² + 6x + 11.

(a) For what value of x does f(x) attain its minimum value?

(b) Sketch the graph.

(c)  Find the vertex of the graph of f .

Solution :

In order to convert the given quadratic function into vertex form, let us use the method completing the square method.

Let y = x² + 6x + 11

y - 11  =  x² + 6x

y - 11  =  x² + 2 ⋅ x ⋅ 3 + 3² - 3²

y - 11  =  (x + 3)² - 9

y  =  (x + 3)² - 9 + 11

y  =  (x + 3)² + 2

y = a(x - h)² + k

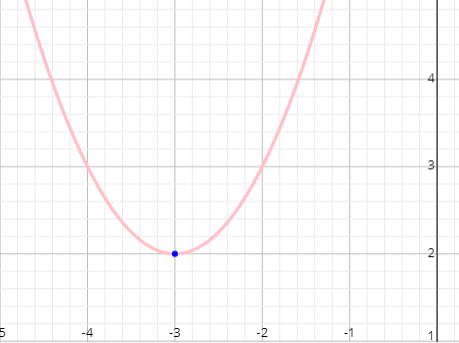
a =  1 > 0, the parabola is open upward, then it will have minimum value. Vertex of parabola (h, k) is (-3, 2)

When x = -3, f(x) attains its minimum value.

(b)  

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.