FINDING INVERSE OF A MATRIX USING FORMULA
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
What is inverse of a matrix ?
For a square matrix A, the inverse is written A-1. When A is multiplied by A-1 the result is the identity matrix I. Non square matrices do not have inverses.
Note: Not all square matrices have inverses. A square matrix which has an inverse is called invertible or nonsingular, and a square matrix without an inverse is called non invertiable or singular.
Formula to find the inverse of the matrix :
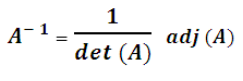
Example 1 :
Find the inverse of the following matrix
|
Solution :
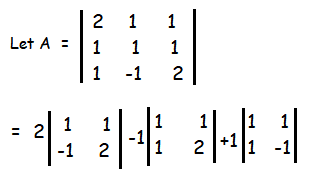
|A| = 2(2+1) - 1(2-1) + 1(-1-1)
|A| = 2(3) - 1(1) + 1(-2)
|A| = 6-1-2
|A| = 3 ≠ 0
Since A is a non singular matrix. A-1 exists.

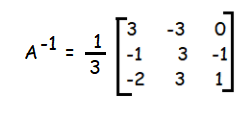
Example 2 :
Find the inverse of the following matrix
|
Solution :
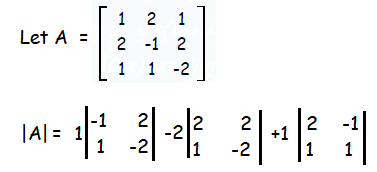
|A| = 1(2-2)-2(-4-2)+1(2+1)
= 1(0) - 2(-6)+1(3)
= 12 + 3
|A| = 15 ≠ 0
Since A is a non singular matrix. A-1 exists.

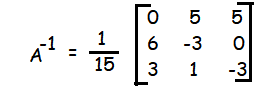
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
10 Hard SAT Math Questions (Part - 44)
Jan 12, 26 06:35 AM
10 Hard SAT Math Questions (Part - 44) -
US Common Core K-12 Curricum Algebra Solving Simple Equations
Jan 07, 26 01:53 PM
US Common Core K-12 Curricum Algebra Solving Simple Equations -
10 Hard SAT Math Questions (Part - 4)
Jan 05, 26 06:56 PM
10 Hard SAT Math Questions (Part - 4)
