FINDING INVERSE OF A FUNCTION

Question 1 :

Suppose f(x) = 2x + 3.

(a) Evaluate f⁻¹(11).

(b) Find a formula for f⁻¹(y).

Solution :

In order to find the inverse function, first let us prove the given function is one to one.

The domain of the function f(x) is all real values, each real values of x is associated with unique elements of y. So it is one to one function.

 y  =  f(x)  =  2x + 3

 2x + 3  =  y

2x  =  y - 3

x  =  (y - 3)/2

Replace x by f^-1 (y) and y by x.

f^-1(y)  =  (y - 3)/2

Question 2 :

Suppose the domain of f is the interval [0, 2], with f defined on this domain by the equation f(x) = x². 

(a) What is the range of f ?

(b) Find a formula for the inverse function f ⁻¹.

(c) What is the domain of the inverse function f ⁻¹?

(d) What is the range of the inverse function f ⁻¹?

Solution :

f(x) = x²

From this, we know that range is [0, 4].

(b) Find a formula for the inverse function f ⁻¹.

From the table given above, we know that each values is associated with unique elements. So it is one to one.

y = x²

x  =  √y

Here x can be replaced by f^-1(y), so f^-1(y)  =  √y

(c) What is the domain of the inverse function f ⁻¹?

Domain of f ⁻¹  =  Range of f  =  [0, 4]

(d) What is the range of the inverse function f ⁻¹?

Range of f ⁻¹  =  Domain of f  =  [0, 2]

Question 3 :

The surface area A (in square meters) of a person with a mass of 60 kilograms can be approximated by

A = 0.2195 h^0.3964

where h is the height (in centimeters) of the person.

a. Find the inverse function. Then estimate the height of a 60-kilogram person who has a body surface area of 1.6 square meters.

b. Verify that function A and the inverse model in part  (a) are inverse functions

Solution :

A = 0.2195 h^0.3964

Finding inverse function :

A/0.2195 = h^0.3964

h = (A/0.2195)^1/0.3964

a) When A = 1.6 square meter, h = ?

h = (1.6/0.2195)^1/0.3964

h = (7.289)^2.522

h = 149.8

Approximately 150 cm.

Question 4 :

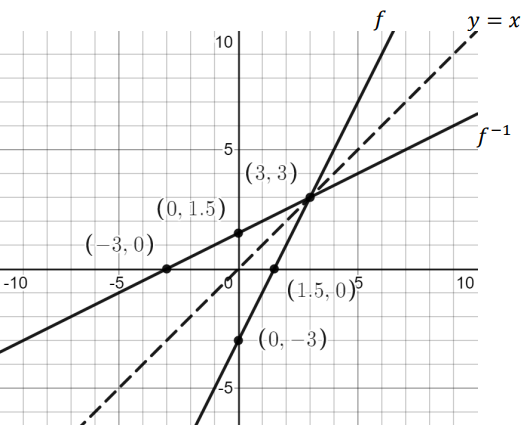
𝒇(𝒙) = 𝟐𝒙 − 𝟑

a) Determine 𝑓 −1 (𝑥)

b) Show that 𝑓(𝑓 ⁻¹ (𝑥)) = 𝑓 ⁻¹ (𝑓(𝑥)) = 𝑥

c) Graph 𝑓 𝑎𝑛𝑑 𝑓 −1

Solution :

a)

𝒇(𝒙) = 𝟐𝒙 − 𝟑

Let y = 2x - 3

y + 3 = 2x

x = (1/2)(y + 3)

Put x = 𝑓 ⁻¹ (𝑥) and y = x

𝑓 ⁻¹ (𝑥) = (1/2)(x + 3)

b) 𝑓(𝑓 ⁻¹ (𝑥))

Applying the 𝑓 ⁻¹ (𝑥) in the function f(x).

𝑓((1/2)(x + 3)) = 2(1/2)(x + 3) - 3

= x + 3 - 3

= x -----(1)

𝑓 ⁻¹ (𝑓(𝑥)) = 𝑓 ⁻¹ (2x + 3)

Applying the value of f(x) in 𝑓 ⁻¹ (x)

= 2(x/2 + 3/2) - 3

= x + 3 - 3

= x  -----(2)

(1) = (2)

Question 5 :

Answer the following. Assume that f is a one-to-one function.

a)  f(4) = 5, find f^-1(5)

b)  f(3) = 9 and f(9) = 5, find f^-1(9)

Solution :

a)  Given that f(4) = 5

f^-1(5) = 4

b)  Given that f(3) = 9 and f(9) = 5

For the function f(x) :

• When x = 3, y = 9
• When x = 9, y = 5
• (3, 9) and (9, 5).

f^-1(9) = 3

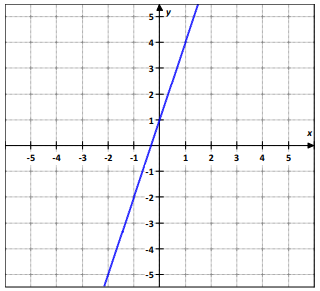
Question 6 :

Use the graph of each function to graph its inverse function. 

f(x) = 3x + 1

Solution :

Some of the points on the line,

(0, 1) (1, 4) (-1, -2) (-2, -5)

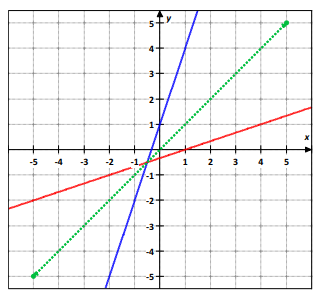
Finding points on the inverse function :

(1, 0) (4, 1) (-2, -1) and (-5, -2)

Determine whether each function has an inverse function. If it does, find the inverse function and state any restrictions on its domain.

Question 7 :

f(x) = (4x - 1)/(x - 1)

Solution :

y = (4x - 1) / (x - 1)

• Domain of the function f(x) is (-∞, 1) and (1, ∞).
• Range of the function f(x) is (-∞, 4) and (4, ∞).

y(x - 1) = 4x - 1

xy - y = 4x - 1

xy - 4x = y - 1

x(y - 4) = y - 1

x = (y - 1)/(y - 4)

So, the required inverse function is

f^-1(x) = (x - 1)/(x - 4)

Domain and range of inverse function :

• Domain of the function f(x) is (-∞, 4) and (4, ∞).
• Range of the function f(x) is (-∞, 1) and (1, ∞).

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.