FINDING FACTORS OF A NUMBER

Example 1 :

Find the factors of 45 

Solution :

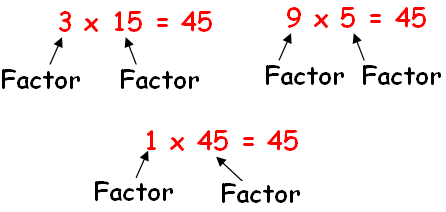
Factors of 45 are 1, 3, 5, 9, 15, 45. 

Example 2 :

Write the factors of 15.

Solution :

15  =  1 x 15

15  =  5 x 3

Factors of 15 are 1, 3, 5 and 15.

Example 3 :

Write the factors of 18.

Solution :

18  =  1 x 18

18  =  2 x 9

18  =  3 x 6

Factors of 18 are 1, 2, 3, 6, 9 and 18.

Example 4 :

Write the factors of 35.

Solution :

35  =  1 x 35

35  =  5 x 7

Factors of 35 are 1, 5, 7 and 35.

Example 5 :

Write the factors of 120.

Solution :

120  =  1 x 120

120  =  2 x 60

120  =  3 x 40

120  =  4 x 30

120  =  5 x 24

120  =  6 x 20

120  =  8 x 15

120  =  10 x 12

120  =  12 x 10

Factors of 120 are 1, 2, 3, 4, 5, 6, 8, 10, 12 and 120.

Example 6 :

Lance has some cards. This number of cards is a multiple of 2 and 5. How many cards could Lance have?

a) 14    b) 15     c) 20     d)  25

Solution :

Since the number of cards is a multiple of 2 and 5, it must be the multiple of 10.

Multiples of 10 are 10, 20, 30, ............

So, option c is correct.

Example 7 :

Which of the following is the factor of 72?

a)  8 and 9     b)  12 and 7     c)  36 and 36      iv) 9 and 7

Solution :

To get the factors of 72, let us try to write the given number as product of 2 numbers.

72 = 2 x 36

72 = 4 x 18

72 = 8 x 9

So, option a is correct.

Example 8 :

Product of first three prime number is

a)  20    b)  30     c)   40     d)  6

Solution :

The first three prime numbers are

2, 3, 5

Product of these three = 2 x 3 x 5

= 30

So, option b is correct.

Example 9 :

H.C.F of two prime number is__________. 

Solution :

Let us consider any two prime numbers, for example 

3 and 5

The common number which divides these two will be 1.

HCF of 3 and 5 is 1

The least number which can be divided by these two numbers is 15

LCM = 3 x 5 ==> 15

So, the H.C.F of two prime numbers is 1.

Example 10 :

The prime factorization of 72  is____________________

Solution :

To find the prime factors of the given number, we have to divide the given numbers only by the prime number.

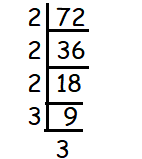
72 = 2 x 2 x 2 x 3 x 3

Since we have repeating factors, we can write it in exponential form.

72 = 2³ x 3²

Example 11 :

Do the prime factorization of largest 3-digit number.

Solution :

The largest 3 digit number is 999

Using divisibility rule for 3,

9 + 9 + 9 = 27

Here 27 is divisible by 3, then 999 is also divisible by 3.

999 = 3 x 3 x 111

= 3² x 111

Find all factor pairs for each number below using your divisibility rules.

Example 12 :

Factor Pairs of 20

Solution :

Using divisibility rules,

Divisible by 2 : 

A number which ends with 0, 2, 4, 6 or 8, it must be divisible by 2.

So, 20 is divisible by 2.

20 = 2 x 10

Divisible by 4 :

If the last two digits is divisible by 4, then the given number is also divisible by 4.

20 = 4 x 5

Every number is factor of 1.

20 = 1 x 20

So, the factors are 1, 2, 4, 5, 20

Example 13 :

Find the product of all the factors of 40. 

Solution :

Factors of 40 are 

2 x 20, 4 x 10, 5 x 8 and 1 x 40

So, factors are 1, 2, 4, 5, 8, 20, 40

Product of these factors :

1 x 2 x 4 x 5 x 8 x 20 x 40

= 256000

Then the product of factors of 40 is 256000.

Example 13 :

Find the greatest 3-digit number which is divisible by 10 and 20.

Solution :

To find the greater 3 digit number which is divisible by 10 and 20, we have to find the lcm of 10 and 20.

20 is the lcm of 10 and 20.

Multiples of 20 are

20, 40, 60, 80, 100, .......................980

So, the greatest 3 digit number which is divisible by 10 and 20 is 980.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.