EQUATION OF MEDIAN OF A TRIANGLE
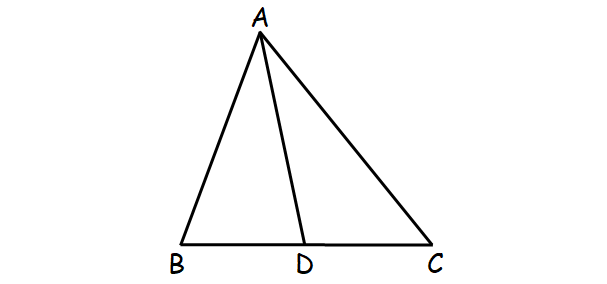
In a triangle, median is a line segment joining a vertex to the midpoint of the corresponding opposite side. There are three medians for a triangle.
In ΔABC shown below, D is the midpoint of side BC and AD is the median through the vertex A.
We can find the equation of median as explained below.
Step 1 :
Using midpoint formula, find the midpoint of BC, which is D.
Step 2 :
Find the slope of median AD using the points A and D.
Step 3 :
Using point-slope form equation y - y1 = m(x - x1), find the equation of the median AD.
Note :
When point-slope form is used to find the equation of median, usually the point at the vertex is taken.
Example 1 :
Find the equations of three medians of ΔABC with vertices A(1, -3), B(-2, 5) and C(-3, 4).
Solution :
Let D, E and F be the midpoints of the sides AB, BC, and AC respectively.
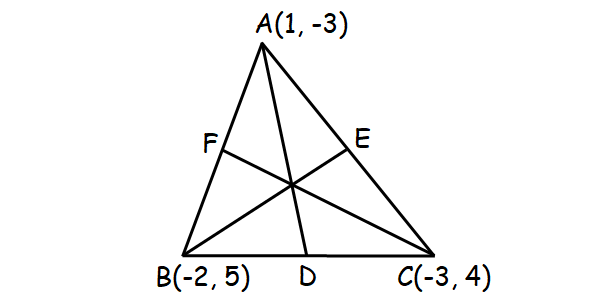
Equation of Median AD :
Midpoint of BC :
= ((x1 + x2)/2, (x1 + x2)/2)
Substitute (x1, y1) = B(-2, 5) and (x2, y2) = C(-3, 4).
= D((-2 - 3)/2, (5 + 4)/2)
= D(-5/2, 9/2)
Slope of AD :
= (y2 - y1)/(x2 - x1)
Substitute (x1, y1) = A(1, -3) and (x2, y2) = D(-5/2, 9/2).
= (9/2 + 3)/(-5/2 - 1)
= (15/2)/(-7/2)
= -15/7
Equation of median AD :
y - y1 = m(x - x1)
Substitute (x1, y1) = A(1, -3) and m = -15/7.
y + 3 = (-15/7)(x - 1)
7(y + 3) = -15(x - 1)
7y + 21 = -15x + 15
15x + 7y + 6 = 0
Equation of Median BE :
Midpoint of AC :
= ((x1 + x2)/2, (x1 + x2)/2)
Substitute (x1, y1) = A(1, -3) and (x2, y2) = C(-3, 4).
= E((1 - 3)/2, (-3 + 4)/2)
= E(-1, 1/2)
Slope of BE :
= (y2 - y1)/(x2 - x1)
Substitute (x1, y1) = B(-2, 5) and (x2, y2) = E(-1, 1/2).
= (1/2 - 5)/(-1 + 2)
= (-9/2)/1
= -9/2
Equation of median BE :
y - y1 = m(x - x1)
Substitute (x1, y1) = B(-2, 5) and m = -9/2.
y - 5 = (-9/2)(x + 2)
2(y - 5) = -9(x + 2)
2y - 10 = -9x - 18
9x + 2y + 8 = 0
Equation of Median CF :
Midpoint of AB :
= ((x1 + x2)/2, (x1 + x2)/2)
Substitute (x1, y1) = A(1, -3) and (x2, y2) = B(-2, 5).
= F((1 - 2)/2, (-3 + 5)/2)
= E(-1/2, 1)
Slope of CF :
= (y2 - y1)/(x2 - x1)
Substitute (x1, y1) = C(-3, 4) and (x2, y2) = F(-1/2, 1).
= (1 - 4)/(-1/2 + 3)
= -3/(5/2)
= -6/5
Equation of median CF :
y - y1 = m(x - x1)
Substitute (x1, y1) = C(-3, 4) and m = -6/5.
y - 4 = (-6/5)(x + 3)
5(y - 4) = -6(x + 3)
5y - 20 = -6x - 18
6x + 5y - 2 = 0
Example 2 :
If the vertices of triangle ABC are A (-4, 4), B(8, 4) and C(8, 10). Find the equation of the line along the median from the vertex A.
Solution :
Let D be the midpoint of the side BC.
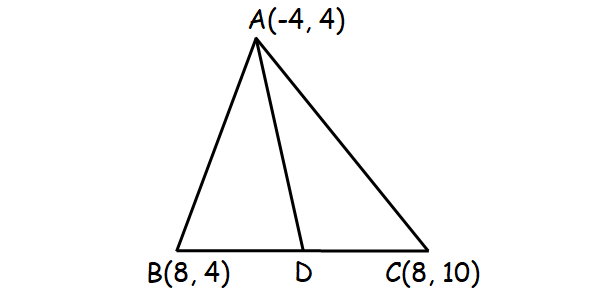
Midpoint of BC :
= ((x1 + x2)/2, (x1 + x2)/2)
Substitute (x1, y1) = B(8, 4) and (x2, y2) = C(8, 10).
= D((8 + 8)/2, (4 + 10)/2)
= D(8, 7)
Slope of AD :
= (y2 - y1)/(x2 - x1)
Substitute (x1, y1) = A(-4, 4) and (x2, y2) = D(8, 7).
= (7 - 4)/(8 + 4)
= 3/12
= 1/4
Equation of the line along the median from the vertex A :
y - y1 = m(x - x1)
Substitute (x1, y1) = A(-4, 4) and m = 1/4.
y - 4 = (1/4)(x + 4)
4(y - 4) = 1(x + 4)
4y - 16 = x + 4
x - 4y + 20 = 0
Example 3 :
The vertices of ∆ PQR are P(2, 1), Q(−2, 3) and R (4, 5). Find the equation of the median through the vertex R.
Solution :
Median which passes through vertex R will divide the opposite side into two equal parts.
Midpoint = (2 + (-2)) / 2, (1 + 3)/2
= (0/2, 4/2)
= S (0, 2)
Equation of the line joining the points R (4, 5) and S (0, 2)
Slope of RS :
= (2 - 5) / (0 - 4)
= -3/(-4)
= 3/4
Slope of the line RS = 3/4
Equation of median line :
y = mx + b
2 = (3/4) (0) + b
b = 2
y = (3/4) x + 2
Example 4 :
For triangle A(-6, 6) B(4, -4) C(2, 10) find the equation of the median from vertex B (start by making a rough sketch of the median on the diagram) :
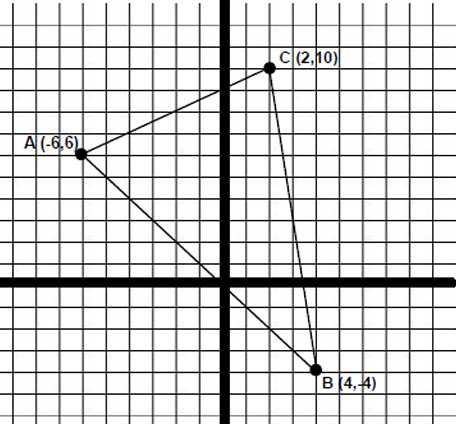
The median drawn from the point B will bisect the side AC. The midpoint of AC is D.
Midpoint of AC = (-6 + 2)/2, (6 + 10)/2
= -4/2, 16/2
= D (-2, 8)
Slope of BD :
B(4, -4) and D(-2, 8)
Slope = (8 - (-4)) / (-2 - 4)
= (8 + 4) / (-6)
= 12/(-16)
= -2
Equation of median BD :
(y - y1) = m(x - x1)
y + 4 = -2(x - 4)
y = -2x + 8 - 4
y = -2x + 4
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
10 Hard SAT Math Questions (Part - 34)
Nov 15, 25 08:00 AM
10 Hard SAT Math Questions (Part - 34) -
Algebra Word Problems Worksheet with Answers
Nov 10, 25 06:30 PM
Algebra Word Problems Worksheet with Answers -
Tricky SAT Math Problems Solved Easily
Nov 09, 25 07:02 PM
Tricky SAT Math Problems Solved Easily