FINDING AXIS OF SYMMETRY OF PARABOLA

The axis of symmetry of a parabola is a line about which the parabola is symmetrical. When the parabola is vertical, the line of symmetry is vertical.

When a quadratic function is graphed in the coordinate plane, the resulting parabola and corresponding axis of symmetry are vertical.

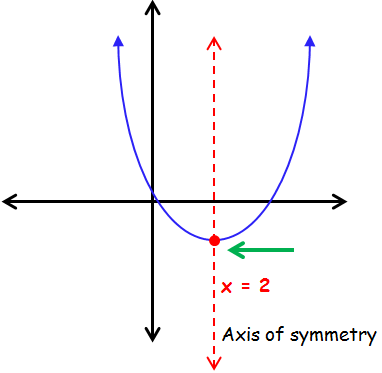
If a quadratic function is y = ax² + bx + c, then its axis of symmetry has equation

x = -b/2a

Example 1 :

Find the equation of the axis of symmetry of

y  =  2x²+3x+1

Solution :

y  =  2x² +3x +1

Here a  =  2, b  =  3 and c  =  1

Axis of symmetry  =  -b/2a

x  =  -3/2(2)

x  =  -3/4

Example 2 :

Find the equation of the axis of symmetry of

y  =  -x²-4x+1

Solution :

y  =  -x²-4x+1

Here a  =  -1, b  =  -4 and c  =  1

Axis of symmetry  =  -b/2a

x  =  -(-4)/2(-1)

x  =  4/(-2)

x  =  -2

Example 3 :

Find the equation of the axis of symmetry of

y  =  (1/2)x²-10x+2

Solution :

y  =  (1/2)x²-10x+2

Here a  =  1/2, b  =  -10 and c  =  2

Axis of symmetry  =  -b/2a

x  =  -(-10)/2(1/2)

x  =  10

Example 4 :

Find the equation of the axis of symmetry of

y  =  (1/3)x²+4x

Solution :

y  =  (1/3)x²+4x

Here a  =  1/3, b  =  4 and c  =  0

Axis of symmetry  =  -b/2a

x  =  -4/2(1/3)

x  =  -4 ⋅ (3/2)

x  =  -6

Example 5 :

Find the equation of the axis of symmetry of

y  =  100x-4x²

Solution :

y  =  -4x²+100x

Here a  =  -4, b  =  100 and c  =  0

Axis of symmetry  =  -b/2a

x  =  -100/2(-4)

x  =  25/2

Example 6 :

A fireworks rocket is launched from a hill above a lake. The rocket will fall into the lake after exploding at its maximum height. The rocket's height above the surface of the lake is given by

g(x) = -16x² + 64x + 80

What is the maximum height of the rocket?

A) 150 feet  B) 80 feet   C) 120 feet  D) 144 feet

Solution :

g(x) = -16x² + 64x + 80

Since the coefficient of x² is negative, the parabola must be open downward. It must have maximum value at vertex.

Here a = -16, b = 64 and c = 80

x = -b/2a

x = -64/2(-16)

= 64/32

x = 2

Applying the value of x, we get

g(2) = -16(2)² + 64(2) + 80

= -16(4) + 128 + 80

= -64 + 128 + 80

= -64 + 208

= 144

So, the maximum height is 144 feet.

Example 7 :

In an effort to catch a criminal; a superhero is going to leap over a building and take a short cut down the ally. The function

f(x) = -16x² + 150x

gives the superhero's height in feet as a function of time. The building is 425 feet high. Will the superhero make it over the building?

A) Yes, the superhero always makes it!

B) No, the superhero can only jump half the height of the building

C) No, the superhero will crash into the building at 351 feet

D) No, the superhero can only jump 150 feet into the air

Solution :

f(x) = -16x² + 150x

Height of the building = 425

-16x² + 150x

Finding the maximum height,

x = -b/2a

a = -16, b = 150 and c = -425

x = -(-150)/2(-16)

= 150/32

= 4.68

At 4.68 seconds he will reach the maximum height

h(4.68) = -16(4.68)² + 150(4.68)

= -350.43 + 702

= 351.57 feet

The height of the building is 425 feet, but he can reach only 351.57 feet. So, the answer is option C.

Example 8 :

A rock is thrown from the top of a tall building. The distance, in feet, between the rock and the ground x seconds after it is thrown is given by

f(x) = -16x² - 4x + 382

How long after the rock is thrown does it hit the ground?

A) 12.256 seconds    B) 11.50 seconds    C) 4.7324 seconds

D) 7.236 second

Solution :

f(x) = -16x² - 4x + 382

f(x) = 0

-16x² - 4x + 382 = 0

-8x² - 2x + 191 = 0

a = -8, b = -2 and c = 191

= (-b ±√b² - 4ac)/2a

= 2 ± √(-2)² - 4(-8)(191)/2(-8)

= 2 ± √(4 + 6112)/(-16)

= 2 ± √6116/(-16)

x = 4.76 seconds

So, option C is correct.

Example 9 :

A rock is thrown from the top of a tall building. The distance, in feet, between the rock and the ground x seconds after it is thrown is given by

f(x) = -16x² - 4x + 382

How long after the rock is thrown is it 340 feet from the ground?

A) 2.256 seconds     B) 1.50 seconds

C) 3.324 seconds     D) .236 seconds

Solution :

When height = 340 feet

-16x² - 4x + 382 = 340

-16x² - 4x + 382 - 340 = 0

-16x² - 4x + 42 = 0

-8x² - 2x + 21 = 0

a = -8, b = -2 and c = 21

= (-b ±√b² - 4ac)/2a

= 2 ± √(-2)² - 4(-8)(21)/2(-8)

= 2 ± √(4 + 672)/(-16)

= 2 ± √676/(-16)

x = -1.75 and x = 1.5 seconds

x = 4.76 seconds

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.