FINDING AREA OF THE RHOMBUS

Formula for finding area of the rhombus :

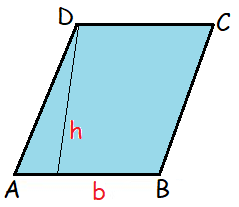
If the area of the rhombus is in terms of its base and height, we will use to below formula.

Area of the rhombus  =  b × h sq.units

Since the rhombus is also like a parallelogram, we can use the same formula to find the area of the parallelogram.

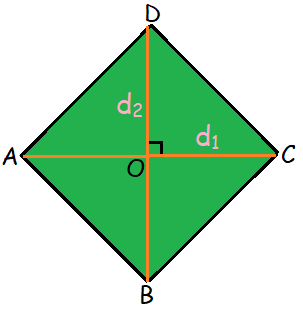
If the area of the rhombus is in terms of its diagonals, we will use to below formula.

Area of the rhombus  = 1/2 × (product of diagonals)

That is,

Area of the rhombus  =  1/2 × d₁ × d₂ sq. units

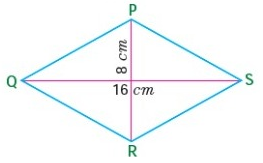
Find the area of rhombus PQRS shown in the following figures.

Problem 1 :

Solution :

From the figure,

Given, d₁  = 8 cm,  d₂  =  16 cm 

Area of the rhombus  =  1/2 x (d₁ x d₂) sq. units

=  1/2 x (8 cm x 16 cm)

=  1/2 x (128 cm²)

=  64 cm²

Problem 2 :

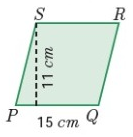
Solution :

From the figure,

Given,  base =  15 cm , height  =  11 cm

Area of the rhombus  =  b x h sq. units

=  15 cm x 11 cm

=  165 cm²

Problem 3 :

Find the area of a rhombus whose base is 14 cm and height is 9 cm.

Solution :

Given, base (b)   =  14 cm

Height (h)  =  9 cm

Area of the rhombus  =  b x h sq. units

=  14 x 9  =  126

Therefore, area of the rhombus  =  126 sq. cm.

Problem 4 :

Find the missing value. 

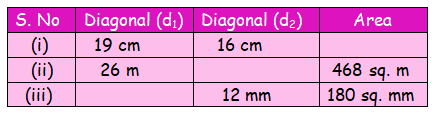
Solution :

(i)

Diagonal (d₁)  =  19 cm

Diagonal (d₂)  =  16 cm

Area of the rhombus  =  1/2 x (d₁ x d₂)

=  1/2  x (19 cm x 16 cm)

=  1/2 x (304 cm²)

=  152 cm²

Therefore, area of the rhombus  =  152 cm²

(ii)

Diagonal (d₁)  =  26 m

Diagonal (d₂)  =  ?

Area of the rhombus  =  468 sq. m

Area of the rhombus  =  1/2 x (d₁ x d₂)

468  =  1/2 x (26 x d₂)

468  =  13 x d₂

468/13  =  d₂

d₂  =  36 m

(iii)

Diagonal (d₁)  =  ?

Diagonal (d₂)  =  12 mm

Area of the rhombus  =  180 sq. mm

Area of the rhombus  =  1/2 x (d₁ x d₂)

180  =  1/2 x (d₁ x 12)

180  =  d₁ x 6

180/6 =  d₁

 d₁  = 30 mm 

Problem 5 :

The area of a rhombus is 100 sq. cm and length of one of its diagonals is 8 cm. Find the length of the other diagonal.

Solution :

Given, the length of one diagonal (d₁)  =  8 cm

Let, the length of the other diagonal be (d₂) cm

Area of the rhombus =  100 sq. cm

Area of the rhombus  =  1/2 x (d₁ x d₂)

100  =  1/2 x (8 x d₂)

100 x 2  =  8 x d₂

200  =  8 x d₂

200/8  =  d₂

25  =  d₂

Therefore, the length of the other diagonal is 25 cm.

Problem 6 :

A sweet is in the shape of rhombus whose diagonals are given as 4 cm and 5 cm. The surface of the sweet should be covered by an aluminum foil. Find the cost of aluminum foil used for 400 such sweets at the rate of $ 7 per 100  sq. cm.

Solution :

Given, one diagonal (d₁)  =  4 cm

other diagonal (d₂)  =  5cm

Area of one rhombus shaped sweet  =  1/2 x (d₁ x d₂)

=  1/2 x 4 cm x 5 cm

=  10 cm²

Aluminum foil used to cover 400 sweets  =  400 x 10

 =  4000 cm²

Cost of aluminum foil for 100 cm²  =  $7

Cost of aluminum foil for 4000 cm²  =  (4000/100) x 7

=  $280

Therefore, the cost of aluminum foil used  =  $280.

Problem 7 :

If the area of a rhombus is 14504 m² and the ratio of diagonals is 37 : 49 then, find the length of the shorter diagonal.

Solution :

Area of a rhombus = 14504 m²

Length of diagonals = 37x and 49x

Area of rhombus = (1/2) (d₁ x d₂)

(1/2) (37x ⋅ 49x) = 14504

x² = 14504(2) / (37 ⋅ 49)

x² = 16

x = √16

x = 4

37x = 37(4) ==> 148 m

49x = 49(4) ==> 196 m

So, the shorter diagonal is 148 m.

Problem 8 :

If the diagonal of a rhombus of side 15 cm are in the ratio 3 : 4, find the area of rhombus.

a)  54 sq.cm     b)  108 sq.cm     c)  144 sq.cm

d) 200 sq.cm      e) None of these

Solution :

Side length of rhombus = 15 cm

Since it is the rhombus, all sides will be equal.

Let the diagonals be 3x and 4x.

Area of rhombus = (1/2) (d₁ x d₂)

Diagonals will bisect each other at right angle

3x/2 and 2x are the length of half of diagonals.

(3x/2)² + (2x)² = 15²

(9x²/4) + 4x²= 225

(9x²+ 16x²)/4 = 225

25x²/4 = 225

25x² = 225(4)

x² = 225(4)/25

x² = 9(4)

x = 3(2)

x = 6

Diagonals are 3(6) and 4(6)

That is 18 cm and 24 cm respectively.

Area of rhombus = (1/2) x 18 x 24

= 216 cm²

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.