FINDING AREA IN THE COORDINATE PLANE

We can use familiar area formulas to find areas of polygons in the coordinate plane.

Examples

Example 1 : 

A gardener uses a coordinate grid to design a new garden. The gardener uses polygon WXYZ on the grid to represent the garden. The vertices of this polygon are W(3, 3), X(−3, 3), Y(−3, −3), and Z(3, −3). Each grid unit represents one yard.Find the area of the garden.

Solution : 

Step 1 :

Graph the vertices, and connect them in order.

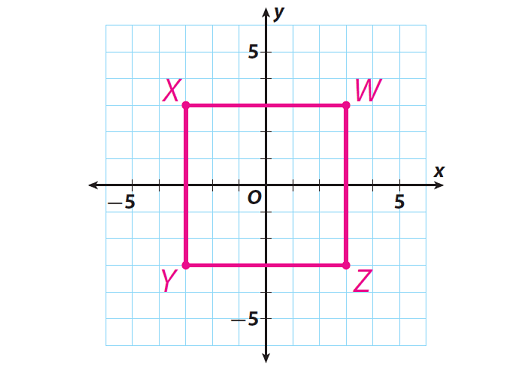
From the graph, it clear that the shape of the garden is a square. 

Let us find lengths of the sides YZ and WZ. 

Step 2 :

Find the length of the side YZ.

The ordered pair of Y is (-3, -3).

The x-coordinate of Y is -3, so point Y is |-3| = 3 yards from the y-axis.

The ordered pair of Z is (3, -3).

The x-coordinate of Z is 3, so point Z is |3| = 3 yards from the y-axis.

Find the sum of the distances :

The length of side YZ  =  3 + 3  =  6 yards

Step 3 :

Find the length of the side WZ.

The ordered pair of W is (3, 3).

The y-coordinate of W is 3, so point W is |3| = 3 yards from the x-axis.

The ordered pair of Z is (3, -3).

The y-coordinate of Z is -3, so point Z is |3| = 3 yards from the x-axis.

Find the sum of the distances :

The length of side WZ  =  3 + 3  =  6 yards.

Step 4 :

Find the area of the square WXYZ using the lengths of the sides YZ and WZ.

Area of the square WXYZ  =  side x side

Area of the square WXYZ  =  YZ x WZ

Area of the square WXYZ  =  6 x 6

Area of the square WXYZ  =  36 square yards

Example 2 : 

Caleb is planning a new deck for his house. He graphs the deck as polygon ABCDEF on a coordinate plane in which each grid unit represents one foot. The vertices of the polygon are A(1, 0), B(3, 2), C(3, 5), D(8, 5), E(8, 2), and F(6, 0). What is the area of Caleb’s deck ?

Solution : 

Step 1 :

Graph the vertices, and connect them in order.

Draw a horizontal dashed line segment to divide the polygon into two quadrilaterals — a rectangle and a parallelogram.

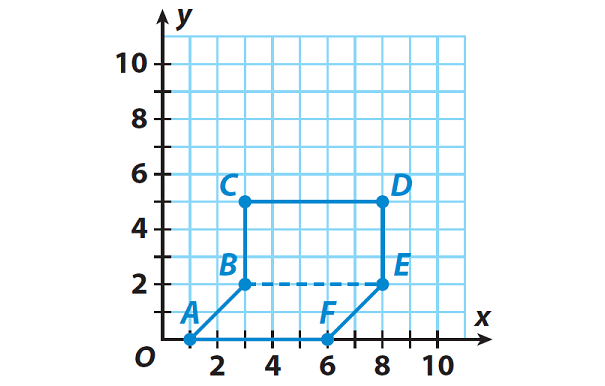
Step 2 :

Find the area of the rectangle using the length of segment BE as the base b and the length of segment BC as the height h.

b  =  |8| − |3|  =  5 feet

h  =  |5| − |2|  =  3 feet

A  =  bh  =  5 x 3  =  15 square feet

Step 3 :

Find the area of the parallelogram using the length of segment AF as the base. Use the length of a segment from F(6, 0) to the point (6, 2) as the height h.

b  =  |6| − |1|  =  5 feet

h  =  |2| − 0  =  2 feet

A  =  bh  =  5 x 2  =  10 square feet

Step 4 :

Add the areas to find the total area of the deck.

hence, the required area is

=  15 + 10  =  25 square feet

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.