FINDING AREA AND PERIMETER OF RECTANGLE EXAMPLES

A rectangle is a special case of a parallelogram in which each pair of adjacent sides is perpendicular. 

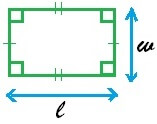
To find area and perimeter of the rectangle, we use the formulas given below.

Area of rectangle  =  length x width

Perimeter of rectangle  =  2 (length + width)

Example 1 :

Find the perimeter of the rectangle.

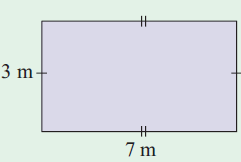
Solution :

Length  =  7 m and width  =  3 m

Perimeter of the rectangle  =  2(7+3)

=  2(10)

=  20 m

So, perimeter of the rectangle is 20 m.

Example 2 :

Find the area of rectangle given below.

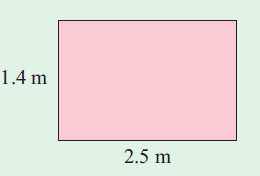
Solution :

Length  =  2.5 m and width  =  1.4 m

Area of rectangle  =  length x width 

=  2.5(1.4)

=  3.5 m²

So, area of rectangle is 3.5 m².

Example 3 :

Find the area and perimeter of the rectangle given below.

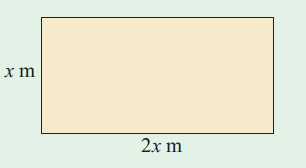
Solution :

length  =  2x and width  =  x

Area of rectangle  =  length ⋅ width

=  2x(x)

=  2x²

So, area of rectangle is 2x² meter square.

Perimeter of the rectangle  =  2(length + width)

=  2(2x+x)

=  2(3x)

=  6x

So, perimeter of the rectangle is 6x meter.

Example 4 :

A rug measuring 2.5 m by 3.5 m was placed in a room 6.4 m long and 8.2 m wide. What area of floor is not covered by the rug?

Solution :

Length of the room  =  6.4 m and width  =  8.2 m

Length of rug  =  3.5 m and width  =  2.5 m

Area of the hall  =  6.4(8.2)

=  52.48 m²

Area covered by rug  =  length ⋅ width

=  3.5(2.5)

=  8.75 m²

Area is not covered by rug  =  52.48-8.75

=  43.73 m²

Example 5 :

A brick wall will be built 56 m long and 10 bricks high. If each brick is 20 cm long, how many bricks will be needed?

Solution :

Length of wall  =  56 m

1 m  =  100 cm

56 m  =  5600 cm

5600/20 ==> 280

280 bricks are needed.

Example 6 :

The school sports fields are laid out in a rectangle 220 m by 160 m. Find the cost of fertilizing the grass if 1 kg of fertilizer covers 80 square meters and fertilizer costs $25 for a 40 kg bag.

Solution :

Area of rectangular field  =  length x width

Length  =  220 m and width  =  160 m

Area of field  =  220(160)

=  35200 square meter 

1 kg of fertilizer covers 80 square meters

=  35200/80

=  440 

Cost of 40 kg bag  =  $25

To number how many 40 kg bags are needed  =  440/40

=  1 1 bags

Cost of 1 bag  =  $25

Required cost  =  11(25)

=  $275

Example 7 :

A carpet measuring 4 m by 3 m is placed in a room 5.2 m long and 4.8 m wide. What area of the floor is left uncarpeted?

Solution :

Length of room  =  5.2 m, width  =  4.8 m

Length of carpet  =  4 m and width  =  3 m

Area of room  =  5.2(4.8)

=  24.96 square meter

Area covered by carpet  =  4(3)

=  12 square meter

Area of floor is left uncarpeted  =  24.96 - 12

=  12.96 square meter

Example 8 :

A lounge room is 5.4 m long, 4.8 m wide, and 4.2 m high. It has a door 2 m by 1 m and a window 2 m by 1.5 m.

a) Draw a diagram to illustrate the room.

b) If wallpaper costs $5.50 per square meter, find the cost of wallpapering the four walls.

Solution :

(a) 

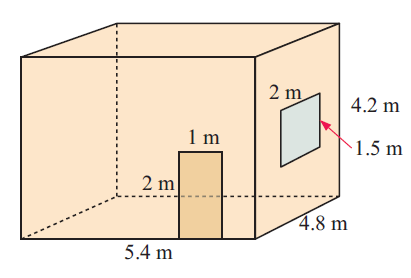
(b)  From the picture :

Area of wall in the left side :

=  (4.8)(4.2)  ==>  20.16  ---(1)

Area of wall in the back side :

=  (5.4)(4.2)  ==>  22.68  ---(2)

Area of wall in the front face except door :

=  5.4(4.2) - 2(1)

=  22.68-2

=  20.68 square meter  ---(3)

Area of wall right side except the window :

=  4.8(4.2) - 2(1.5)

=  20.16-3

=  17.16 square meter  ---(4)

Area covered by wall paper 

=  20.16 + 22.68 + 20.68 + 17.16

=  80.68 square meter

Cost of covering 1 m  =  $5.50

Required cost  =  80.68(5.50)

=  $443.74

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.