FINDING AREA AND PERIMETER OF A PARALLELOGRAM

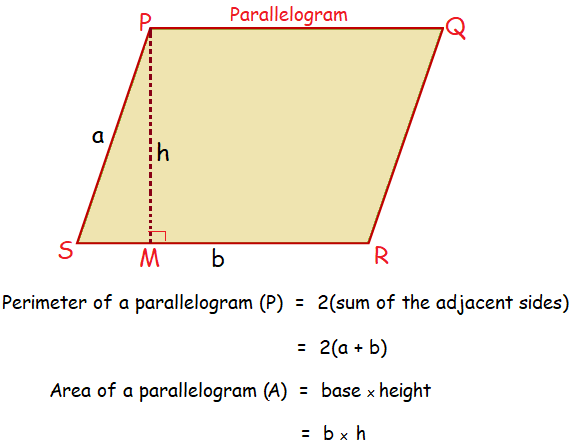
Find the area and perimeter of the following parallelograms :

Problem 1 :

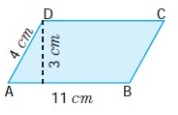
Solution :

From the figure,

Base of a parallelogram (b)  =  11 cm

Height of a parallelogram (h) =  3 cm

Then,

Area of the parallelogram  =  b x h sq. units.

 Area  =  11 x 3

So, area of the parallelogram  =  33 sq. cm.

Perimeter of the parallelogram  =  sum of the length of the four sides.

=  11 cm + 4 cm + 11 cm + 4 cm

So, perimeter of the parallelogram  =  30 cm

Problem 2 :

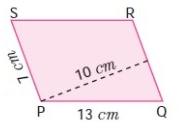
Solution :

From the figure,

Base of a parallelogram (b)  =  7 cm

Height of a parallelogram (h) =  10 cm

Then,

Area of the parallelogram  =  b x h sq. units.

Area  =  7 x 10

So, area of the parallelogram  =  70 sq. cm.

Perimeter of the parallelogram  =  sum of the length of the four sides.

=  13 cm + 7 cm + 13 cm + 7 cm

=  40 cm

Problem 3 :

Find the missing values.

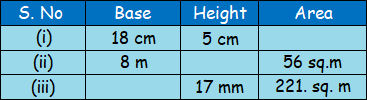
Solution :

(i)

Base of a parallelogram (b)  =  18 cm

Height of a parallelogram (h) =  5 cm

Then,

Area of the parallelogram  =  b x h sq. units.

 Area  =  18 x 5

So, area of the parallelogram  =  90  sq. cm.

(ii)

Base of a parallelogram (b)  =  8 m

Area of the parallelogram  =  56 sq. m

Then,

Area of the parallelogram  =  b x h sq. units.

56  =  8 x h

56/8  =  h

7 m  =  h

So, height of a parallelogram (h)  =  7 m 

(iii)

Height of a parallelogram (h)  =  17 mm

Area of the parallelogram   =  221 sq. mm

Area of the parallelogram  =  b x h sq. units.

221  =  b x 17

221/17  =  b

13 mm  =  b

So, base of a parallelogram (b)  =  13 mm.

Problem 4 :

Suresh won a parallelogram – shaped trophy in a state level chess tournament. He knows that the area of the trophy is 735 sq. cm and its base is 21 cm. what is the height of that trophy?

Solution :

Given,

Base of the trophy (b)  =  21 cm

Area of the trophy   =  735 sq.cm

  Area of the parallelogram  =  b x h sq. units.

735  =  21 x h

735/21  =   h

35 cm  =  h

So, height of trophy (h)  =  35 cm

Problem 5 :

Janaki has a piece of fabric in the shape of a parallelogram. Its height is 12 m and its base is 18 m. She cuts the fabric into four equal parallelograms by cutting the parallel sides through its mid – points. Find the area of each new parallelogram.

Solution :

Given,

Base of a parallelogram (b)  =  18 m

Height of a parallelogram (h)  =  12 m

Area of the parallelogram  =  b x h sq. units.

 =  18 m x 12 m

=  216 m²

Since she cuts the fabric into four equal parallelograms,

=  216/4

 =  54 m²

So, the area of each new parallelogram =  54 m².

Problem 6 :

A ground is in the shape of parallelogram. The height of the parallelogram is 14 meters and the corresponding base is 8 meters longer than its height. Find the cost of levelling the ground at the rate of $ 15 per sq. m.

Solution :

Given,

Base of a parallelogram (b)  =  8 m

Since base is 8 meters longer than height, 

Now, base  =  (14 + 8)  =  22 m

Height of a parallelogram (h)  =  14 m

Area of the parallelogram  =  b x h sq. units.

=  22 m x 14 m

=  308 m²

Cost of levelling 1 m² =  15 per sq. m.

Cost of levelling 308 m²  =  308 x 15

=  $ 4,620

So, the cost of levelling the ground  =  $ 4,620

Problem 7 :

The logo below is created by joining two congruent parallelograms. Calculate the area of the logo. 

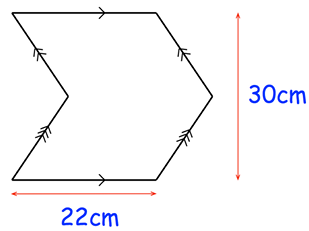
Solution :

Base of parallelogram = 22 cm

height = 30 cm, height of parallelogram = 15 cm

Area of logo = 2 (area of parallelogram)

= 2(base x height)

= 2(22 x 15)

= 660 cm²

Problem 8 :

Find x .

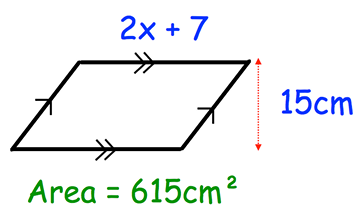
Solution :

Area of parallelogram = 615 cm²

base = 2x + 7, height = 15 cm

(2x + 7) 15 = 615

2x + 7 = 615 / 15

2x + 7 = 41

2x = 41 - 7

2x = 34

x = 34/2

x = 17

So, the value of x is 17.

Problem 9 :

A shape is made from 4 congruent parallelograms. The area of the shape is 792cm²

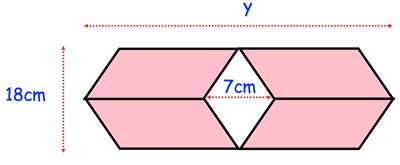
Solution :

height of one parallelogram = 18/2 ==> 9 cm

base = (y - 7)/2

Area of 4 congruent parallelograms = 4 (base x height)

= 4 (9  x (y - 7)/2)

= 18(y - 7)

area of the shape = 792 cm²

18(y - 7) = 792

y - 7 = 792/18

y - 7 = 44

y = 44 + 7

y = 51 cm

So, the value of y is 51 cm.

Problem 10 :

If three consecutive vertices of a parallelogram ABCD are A(1, -2), B(3, 6) and C (5, 10), find its fourth vertex D.

Solution :

In a parallelogram, opposite sides will be equal.

Midpoint of the diagonals will be equal. Let (x, y) be the fourth vertex.

Midpoint of diagonal AC = (x₁ + x₂)/2, (y₁ + y₂)/2

= (1 + 5)/2, (-2 + 10)/2

= 6/2, 8/2

= (3, 4)

Midpoint of diagonal BD = (x₁ + x)/2, (y₁ + y)/2

(3 + x)/2, (6 + y)/2 = (3, 4)

So, the required fourth vertex is at (3, 2).

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.