FINDING A SCALE FACTOR

Example 1 :

An art supply store sells several sizes of drawing  triangles. All are dilations of a single basic triangle. The basic triangle and one of its dilations are shown on the grid. Find the scale factor of the dilation.

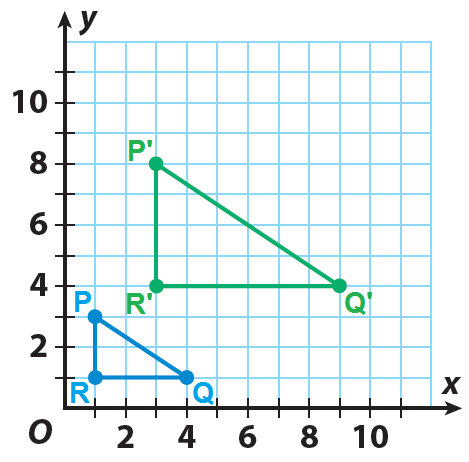
Solution :

Step 1 :

Use the coordinates to find the lengths of the sides of each triangle.

Triangle PQR :

PR  =  2,  RQ  =  3

Triangle P'Q'R' :

P'R'  =  4,  R'Q'  =  6

Step 2 :

Find the ratios of the corresponding sides.

P'R'/PR  =  4/2  =  2

R'Q'/RQ  =  6/3  =  2

Hence, the scale factor of the dilation is 2.

Example 2 :

Find the scale factor of the dilation.

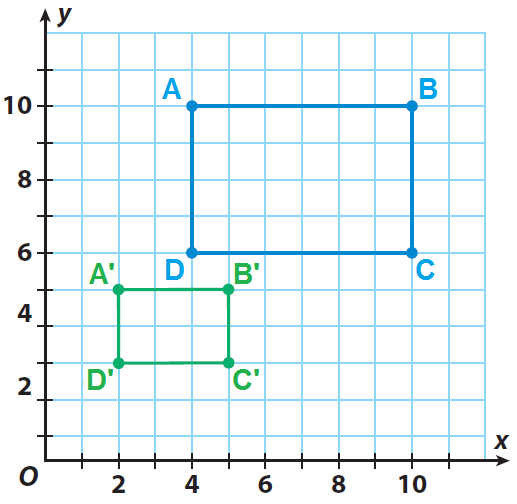
Solution :

Step 1 :

Use the coordinates to find the lengths of the sides of each triangle. 

Since the scale factor is the same for all corresponding sides, we can record just two pairs of side lengths. Use one pair as a check on the other.

Rectangle ABCD :

AB  =  6,  AD  =  4

Rectangle A'B'C'D' :

A'B'  =  3,  A'D'  =  2

Step 2 :

Find the ratios of the corresponding sides.

A'B'/AB  =  3/6  =  0.5

A'D'/AD  =  2/4  =  0.5

Hence, the scale factor of the dilation is 0.5.

Example 3 :

Find the scale factor of the dilation.

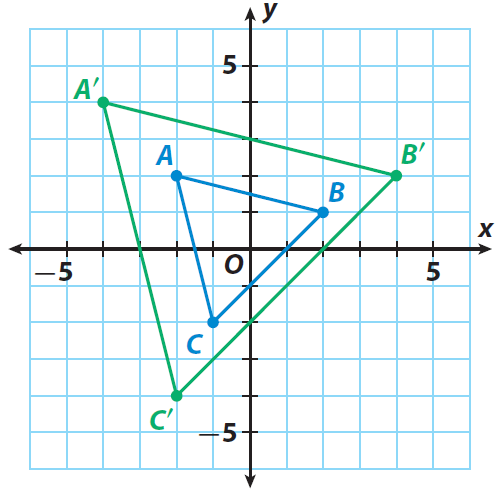
Solution :

Step 1 :

Use the coordinates to find the lengths of the sides of each triangle. 

Since the scale factor is the same for all corresponding sides, we can record just a pair of side lengths. Use one pair as a check on the other.

Since the sides of the triangle and its image after dilation are not parallel to x and y axes, we can use the distance between two points formula to find the lengths of the sides.

Triangle ABC :

AB  =  √17,  AC  =  √17

Triangle A'B'C' :

A'B'  =  √68,  A'C'  =  √68

Step 2 :

Find the ratios of the corresponding sides.

A'B'/AB  =  √68/√17  =  √4  =  2

A'C'/AC  =  √68/√17  =  √4  =  2

Hence, the scale factor of the dilation is 2.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.