FIND VALUES OF FUNCTIONS FROM GRAPHS

Let the point (x, y) be on the graph of a function f. Then, y-is the value of the function for the given value of x.

If (2, 5) is on the graph of a function f(x), then 5 is the value of f(x) at x = 2. That is, 

f(2) = 5

Working Rule to Find Value of a Function From Its Graph

Find the value of a function f(x) when x = a.

Step 1 :

Draw a vertical line through the value 'a' on x-axis.

Step 2 :

Mark the point of intersection of the line x = a and graph of f(x).

Step 3 :

Draw an horizontal line from the point of intersection to y-axis.

Step 4 :

Let the horizontal line meet the y-axis at 'b'.

The value of the function f(x) at x = a is 'b'.

That is, 

f(a) = b

Example 1 :

Use the graph of f(x) shown below to find f(6).

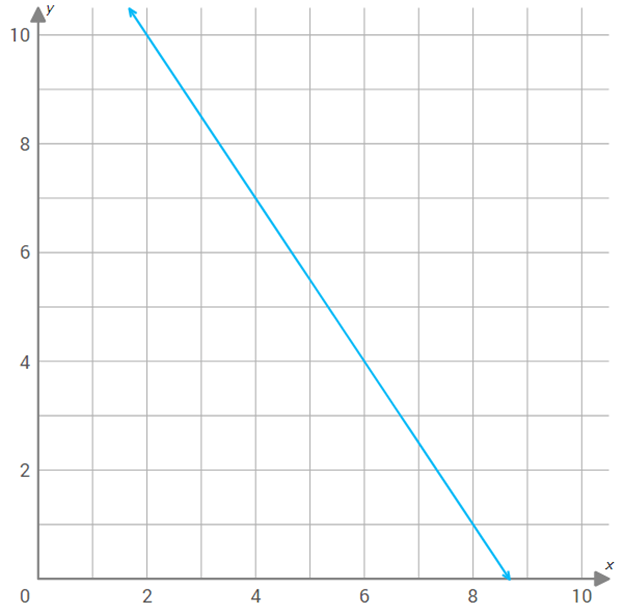
Solution :

We have to find value of the function f(x) at x = 6.

Step 1 :

Draw a vertical line through 6 on the x-axis.

Step 2 :

Mark the point of intersection of the vertical line x = 6 and the graph of f(x).

Step 3 :

Draw an horizontal line from the point of intersection to y-axis.

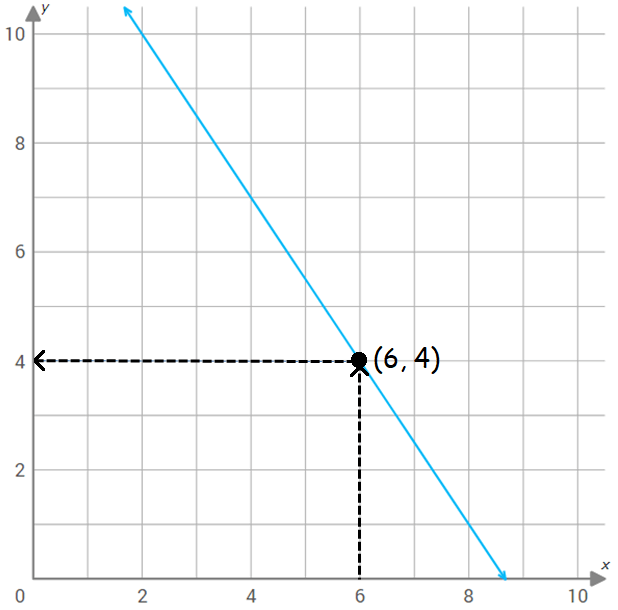
Step 5 :

The horizontal line meets y-axis at 4.

So, the value of the function f(x) at x = 6 is 4.

That is, 

f(6) = 4

Example 2 :

Use the graph of f(x) shown below to find f(9).

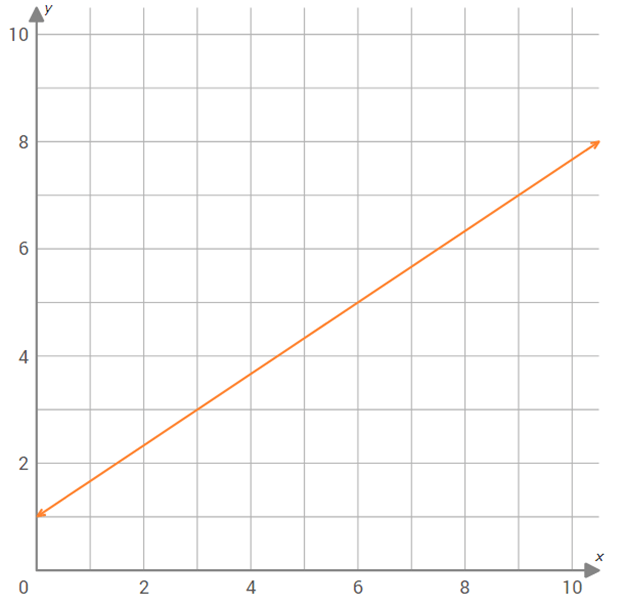
Solution :

We have to find value of the function f(x) at x = 9.

Step 1 :

Draw a vertical line through 9 on the x-axis.

Step 2 :

Mark the point of intersection of the vertical line x = 9 and the graph of f(x).

Step 3 :

Draw an horizontal line from the point of intersection to y-axis.

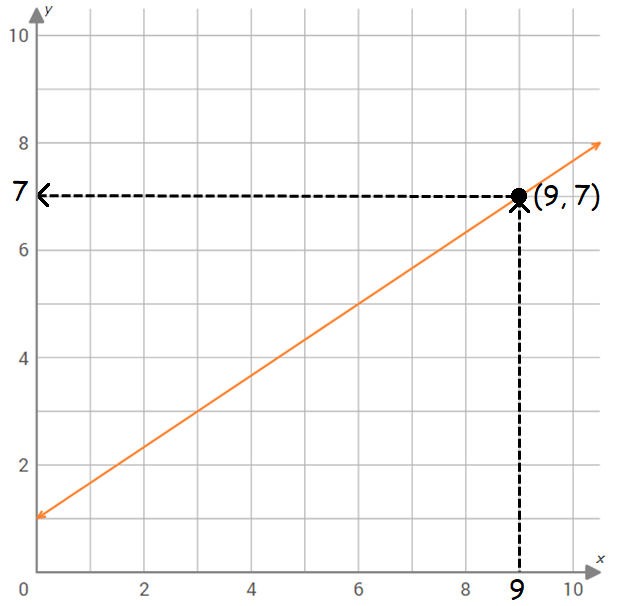
Step 5 :

The horizontal line meets y-axis at 7.

So, the value of the function f(x) at x = 9 is 7.

That is, 

f(9) = 7

Example 3 :

Use the graph of f(x) shown below to find f(4).

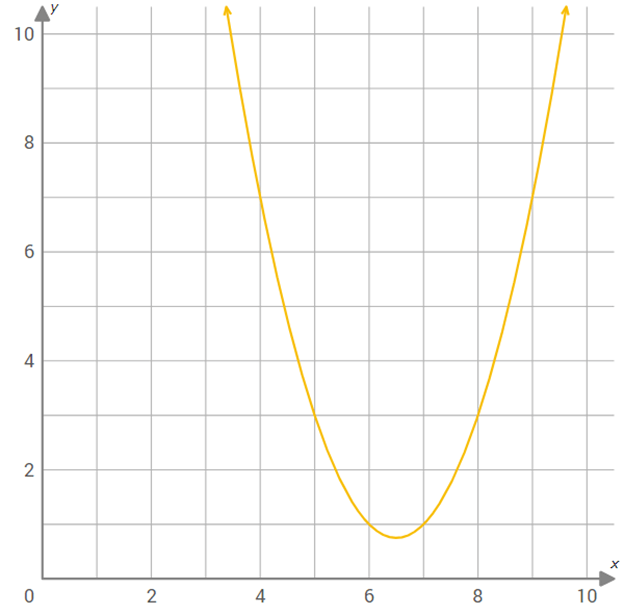
Solution :

We have to find value of the function f(x) at x = 4.

Step 1 :

Draw a vertical line through 4 on the x-axis.

Step 2 :

Mark the point of intersection of the vertical line x = 4 and the graph of f(x).

Step 3 :

Draw an horizontal line from the point of intersection to y-axis.

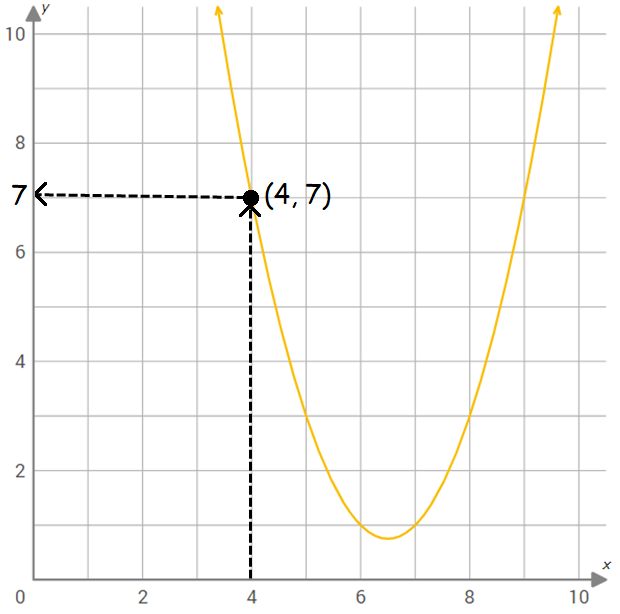
Step 5 :

The horizontal line meets y-axis at 7.

So, the value of the function f(x) at x = 4 is 7.

That is, 

f(4) = 7

Example 4 :

Use the graph of f(x) shown below to find f(4).

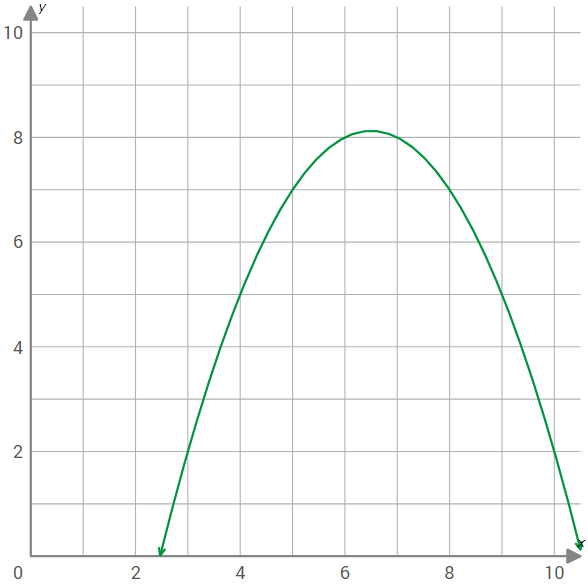
Solution :

We have to find value of the function f(x) at x = 4.

Step 1 :

Draw a vertical line through 4 on the x-axis.

Step 2 :

Mark the point of intersection of the vertical line x = 4 and the graph of f(x).

Step 3 :

Draw an horizontal line from the point of intersection to y-axis.

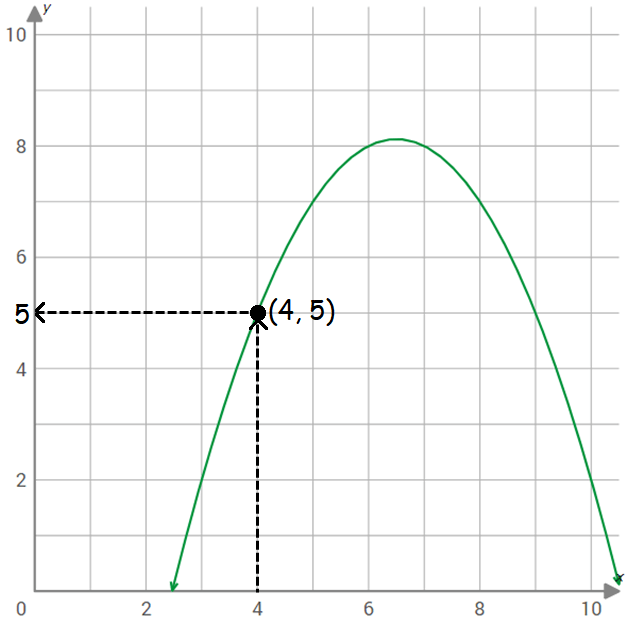
Step 5 :

The horizontal line meets y-axis at 5.

So, the value of the function f(x) at x = 4 is 5.

That is, 

f(4) = 5

Example 5 :

Given this graph of the function f(x)

Find

a)  f(-4)      b)  f(0)       c)  f(3)      d)  f(-5)

e)  x, when f(x) = 2     f)  x, when f(x) = 0

Solution :

a) Drawing the vertical line at -4 on x, we know the vertical line is intersecting the curve at (-4, 2). So, f(-4) = 2.

b)  The vertical line at x = 0, it is intersecting the curve at 0. Then f(0) = 0.

c)  The vertical line at x = 3 is intersecting the curve at -1.5. So, f(3) = -1.5

d)  The vertical line at x = -5 is intersecting the curve at 0. So, f(-5) = 0.

e)  f(x) = 2

Here we should draw the horizontal line at y = 2. The horizontal line at y = 2 is intersecting the curve at -4. So, f(-4) = 2.

f)  f(x) = 0, the horizontal line y = 0 is intersecting the curve at 0. So, when x = 0, then f(x) = 0.

Example 6 :

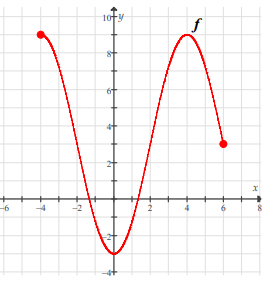
The graph of y = f (x) is shown below.

(a) Find the domain of the function. Write your answer in interval notation.

(b) Find the range of the function. Write your answer in interval notation.

(c) Find the following function values:

f (−2); f (0); f (4); f (6)

(d) For what value(s) of x is f (x) = 9 ?

Solution :

a) The domain is [-4, 6]

b) The range is [-2, 9]

c)  f (−2) = 2, f (0) = -3, f (4) = 9 and f (6) = 3

d) Drawing the horizontal line at x = 9, the curve is intersecting the line at two points, they are -4 and 4. then f(-4) = 9 and f(4) = 9.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.