FIND THE VOLUME OF A PYRAMID

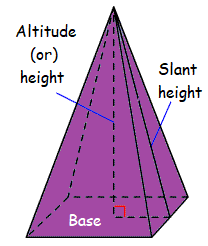
What is a pyramid ?

A 3-dimemsional shape formed by joining all the corners of a polygon to a central point or apex is named as a pyramid.

The base of a pyramid maybe of any shape such as triangle, square, rectangle, hexagonal, etc..

What is volume of a pyramid ?

The volume V of a pyramid is one-third the area of the base B times the height h.

That is,

Volume = 1/3(area of base × height)

Find the volume of the following :

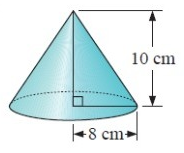
Problem 1 :

Solution :

By observing the figure, it is a cone.

Here area of base is the shape of the circle.

To find the volume,

Volume = 1/3(area of base × height)

= 1/3(area of circle × height)

= 1/3(πr² × height)

we have,

radius (r) = 8 cm and height (h) = 10 cm

= 1/3(π8² × 10)

= 1/3(2009.6)

Volume = 670 cm³

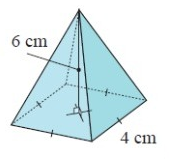
Problem 2 :

Solution :

By observing the figure, it is a square-based pyramid.

Here area of base is the shape of the square.

To find the volume,

Volume = 1/3(area of base × height)

= 1/3(area of square × height)

= 1/3(s² × height)

we have,

side (s) = 4 cm and height (h) = 6 cm

= 1/3(4² × 6)

= 1/3(96)

Volume = 32 cm³

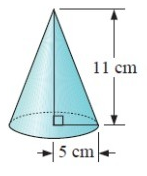
Problem 3 :

Solution :

By observing the figure, it is a cone.

Here area of base is the shape of the circle.

To find the volume,

Volume = 1/3(area of base × height)

= 1/3(area of circle × height)

= 1/3(πr² × height)

we have,

radius (r) = 5 cm and height (h) = 11 cm

= 1/3(π5² × 11)

= 1/3(863.5)

Volume = 288 cm³

Problem 4 :

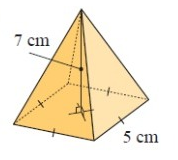
Solution :

By observing the figure, it is a square-based pyramid.

Here area of base is the shape of the square.

To find the volume,

Volume = 1/3(area of base × height)

= 1/3(area of square × height)

= 1/3(s² × height)

we have,

side (s) = 5 cm and height (h) = 7 cm

= 1/3(5² × 7)

= 1/3(175)

Volume = 58.3 cm³

Problem 5 :

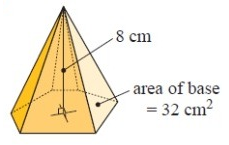
Solution :

By observing the figure, it is a hexagonal pyramid.

Here area of base is the shape of the hexagonal.

To find the volume,

Volume = 1/3(area of base × height)

we have,

area = 32 cm² and height (h) = 8 cm

= 1/3(32 × 8)

= 1/3(256)

Volume = 85.3 cm³

Problem 6 :

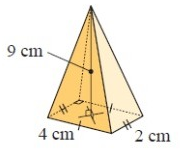
Solution :

By observing the figure, it is a rectangle-based pyramid.

Here area of base is the shape of the rectangle.

To find the volume,

Volume = 1/3(area of base × height)

= 1/3(area of rectangle × height)

= 1/3(length × width × height)

we have,

length (l) = 4 cm, width (w) = 2 cm and height (h) = 9 cm

= 1/3(4 × 2 × 9)

= 1/3(72)

Volume = 24 cm³

Problem 7 :

A square-based pyramid has a base with side length 8 cm. The height of the pyramid is 11 cm. Calculate the volume of the pyramid.

Solution :

Side length of pyramid = 8 cm

Area of pyramid = a²

= 8²

= 64 cm²

Height = 11 cm

Volume of pyramid = (1/3) x base area x height

= (1/3) x 64 x 11

= 234.6 cm³

So, volume of the required square base pyramid is

234.3  cm³

Problem 7 :

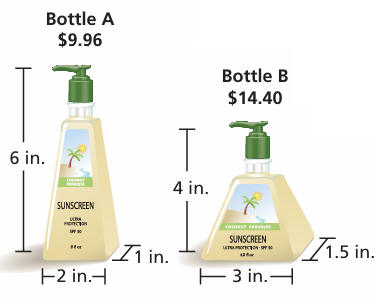
(a) How many times more sunscreen is in Bottle B than in Bottle A?

(b) Which is the better buy?

Solution :

By observing the capacity of sunscreen we can decide.

Quantity of sunscreen in Bottle A :

= (1/3) x base area x height

= (1/3) x (2 x 1) x 6

= (1/3) x 2 x 6

= 4 cubic inches

Quantity of sunscreen in Bottle B :

= (1/3) x base area x height

= (1/3) x (3 x 1.5) x 4

= (1/3) x 2 x 6

= 6 cubic inches.

= 6/4

= 1.5 times

Quantity of sunscreen in Bottle B is 1.5 more than quantity of sunscreen in Bottle A.

b) Cost of 1 square inches of sunscreen in bottle A 

= 9.96/4

= $2.49

Cost of 1 square inches of sunscreen in bottle B 

= 14.40/6

= $2.40

From this, the unit price of bottle B is lesser. Then buying Bottle B is the better buy.

Problem 8 :

In 1483, Leonardo da Vinci designed a parachute. It is believed that this was the first parachute ever designed. In a notebook, he wrote “If a man is provided with a length of gummed linen cloth with a length of 12 yards on each side and 12 yards high, he can jump from any great height whatsoever without injury.” Find the volume of air inside Leonardo’s parachute.

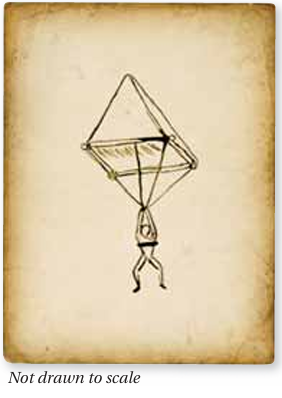
Solution :

Volume of pyramid = (1/3) x base area x height

= (1/3) x 12 x 12 x 12

= 4 x 12 x 12

= 576 cubic yards.

Problem 9 :

Do the two solids have the same volume? Explain.

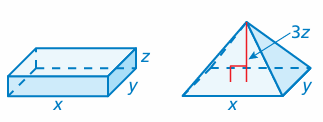
Solution :

Volume of rectangular prism = length x width x height

= x y z

Volume of pyramid = (1/3) xy (3z)

= xyz

Both rectangular prism and pyramid has same volume.

Problem 10 :

How much glass is needed to manufacture 1000 paperweights? Explain your reasoning.

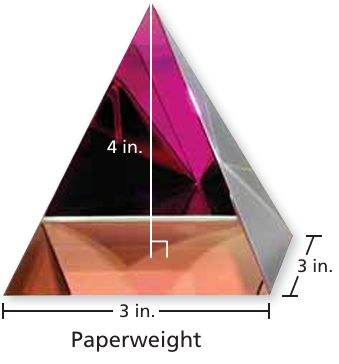
Solution :

Quantity of glass needed to make one paperweight

= (1/3) x 3 x 3 x 4

= 12 cubic inches

Quantity of glass needed to make 1000 = 12 x 1000

= 12000 cubic inches.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.