FIND THE SMALLEST NUMBER WHICH HAS THE GIVEN PRIME FACTORS

Example 1 :

What is the smallest whole number which is the factors of

2, 3 and 5

Solution :

Here the given factors 2, 3 and 5 are prime factors.

=  2 × 3 × 5

=  6 × 5

=  30

So, the required smallest number is 30, which has the factors 2, 3 and 5.

Example 2 :

What is the smallest whole number which is the factors of

3, 5 and 7

Solution :

Here the given factors 3, 5 and 7 are prime factors.

=  3 × 5 × 7

=  15 × 7

=  105

So, the required smallest number is 105, which has the factors 3, 5 and 7.

Example 3 :

What is the smallest whole number which is the factors of

 2, 3, 5 and 7

Solution :

Here the given factors 2, 3, 5 and 7 are prime factors.

=  2 × 3 × 5 × 7

=  30 × 7

=  210

So, the required smallest number is 210, which has the factors 2, 3, 5 and 7.

Example 4 :

List all the factors of each of the following numbers

a)  11, 12, 13, 14, 15, 16, 17, 18, 19, 20

b) Which of these numbers are prime ?

Solution :

a)

• Factors of 11 = 1 and 11
• Factors of 12 = 1, 2, 3, 4, 6 and 12
• Factors of 13 = 1 and 13
• Factors of 14 = 1, 2, 7 and 14
• Factors of 15 = 1, 3, 5 and 15.
• Factors of 16 = 1, 2, 4, 8 and 16
• Factors of 17 = 1 and 17
• Factors of 18 = 1, 2, 3, 6, 9 and 18
• Factors of 19 = 1 and 19
• Factors of 20 = 1, 2, 4, 5, 10 and 20

b) From the list above, we know that some of the numbers has only two factors one and itself. These are prime numbers.

The prime numbers are 11, 13, 17 and 19.

Example 5 :

Explain why 99 is not a prime number.

Solution :

Finding the factors of 99.

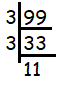
99 = 3 x 3 x 11

The factors are 1, 3, 9 and 11. Since the given number is not having only two factors 1 and 99. It is not a prime number, it is composite number.

Example 6 :

Find the prime factors of 72.

Solution :

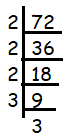
72 = 2 x 2 x 2 x 3 x 3

= 2³ x 3²

So, 2 and 3 are prime factors of 72.

Example 7 :

Find the prime factors that 48 and 54 have in common.

Solution :

Factored form of 48 = 3 x 2 x 2 x 2 x 2

= 3 x 2⁴

Factored form of 54 = 3 x 3 x 3 x 2

= 2 x 3³

Comparing these two, 2 and 3 is in common. So, their product 6 is the common factor.

Example 8 :

Find the prime factors that 40 and 70 have in common.

Solution :

Factored form of 40 = 2 x 2 x 2 x 5

= 2³ x 5

Factored form of 70 = 7 x 2 x 5

Comparing these two, 2 and 5 is in common. So, the common factors of 40 and 70 is 2 and 5.

Example 9 :

Find the prime factors that 40 and 70 have in common.

Solution :

Factored form of 40 = 2 x 2 x 2 x 5

= 2³ x 5

Factored form of 70 = 7 x 2 x 5

Comparing these two, 2 and 5 is in common. So, the common factors of 40 and 70 is 2 and 5.

Example 10 :

A number is expressed as the product of prime factors as 

2³ x 3² x 5

What is the number ?

Solution :

Factored form of the given number = 2³ x 3² x 5

By combining these numbers, we get the original number. That is 

= 8 x 9 x 5

= 360

So, 360 is the required number.

Example 11 :

Which is the smallest number that has

a) 4 different prime factors

b) 5 prime factors

Solution :

a)  Since we are creating the smallest number, we have to use small prime numbers. Choosing 4 primes numbers which are small.

2, 3, 5 and 7

While multiplying that, we get

= 2 x 3 x 5 x 7

= 210

So, the required smallest number which is created using 4 prime factors is 210.

b)  Choosing 5 primes numbers which are small.

2, 3, 5, 7 and 11

While multiplying that, we get

= 2 x 3 x 5 x 7 x 11

= 2310

So, the required smallest number which is created using 5 prime factors is 2310.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.