FIND THE SLOPE FROM TWO POINTS

When the two points (x₁, y₁) and (x₂, y₂) on the line are known, the formula given below can be used to find the slope of the line. 

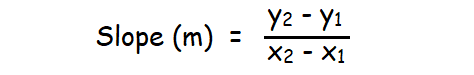
Example 1 :

Find the slope of the line that is passing through the points (1, 12) and (10, 7).

Solution :

Formula :

Slope  =  (y₂ - y₁) / (x₂ - x₁)

Substitute (x₁, y₁) = (1, 12) and (x₂, y₂) = (10, 7). 

Slope  =  (7 - 12) / (10 - 1)

Slope  =  -5/9

Example 2 :

Find the slope of the line that is passing through the points (-2, 0) and (0, 4).

Solution :

Formula :

Slope  =  (y₂ - y₁) / (x₂ - x₁)

Substitute (x₁, y₁) = (-2, 0) and (x₂, y₂) = (0, 4). 

Slope  =  (4 - 0) / [0 - (-2)]

Slope  =  4 / 2

Slope  =  2

Example 3 :

Find the slope of the line that is passing through the points (3, 2) and (8, 4).

Solution :

Slope  =  (y₂ - y₁) / (x₂ - x₁)

Substitute (x₁, y₁) = (3, 2) and (x₂, y₂) = (8, 4). 

Slope  =  (4 - 2) / (8 - 3)

Slope  =  2 / 5

Example 4 :

Find the slope of the line that is passing through the points (1, -1) and (2, 1).

Solution :

Slope  =  (y₂ - y₁) / (x₂ - x₁)

Substitute (x₁, y₁) = (1, -1) and (x₂, y₂) = (2, 1). 

Slope  =  [1 - (-1)] / (2 - 1)

Slope  =  [1 + 1] / 1

Slope  =  2 / 1

Slope  =  2

Example 5 :

Find the slope of the line that is passing through the points (-2, -2) and (-1, 3). 

Solution :

Slope  =  (y₂ - y₁) / (x₂ - x₁)

Substitute (x₁, y₁) = (-2, -2) and (x₂, y₂) = (-1, 3). 

Slope  =  [3 - (-2)] / [-1 - (-2)]

Slope  =  [3 + 2] / [-1 + 2]

Slope  =  5 / 1

Slope  =  5

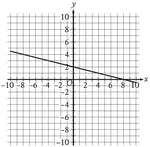
Example 6 :

Find the slope of the line using formula. 

Solution :

Mark two points on the line such that both the x-coordinate and y-coordinate are integers. 

So, we can mark the points (1, -1) and (4, 3) and measure the rise and run.

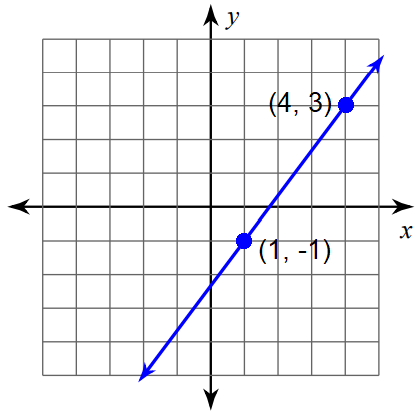
Formula :

Slope  =  (y₂ - y₁) / (x₂ - x₁)

Substitute (x₁, y₁) = (1, -1) and (x₂, y₂) = (4, 3). 

Slope  =  [3 - (-1)] / (4 - 1)

Slope  =  [3 + 1] / 3

Slope  =  4/3

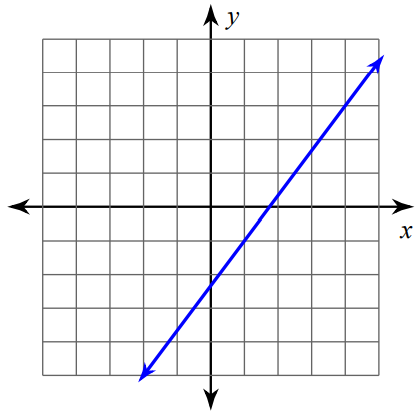
Example 7 :

Find the slope of the line using formula. 

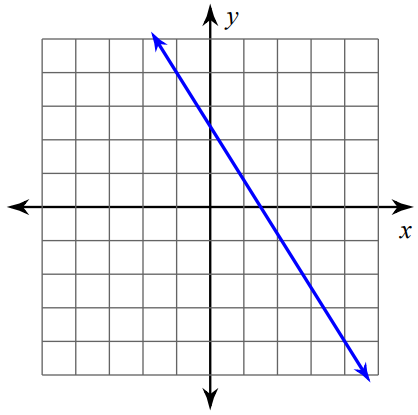
Solution :

Mark two points on the line such that both the x-coordinate and y-coordinate are integers. 

So, we can mark the points (-1, 4) and (4, -4) and measure the rise and run.

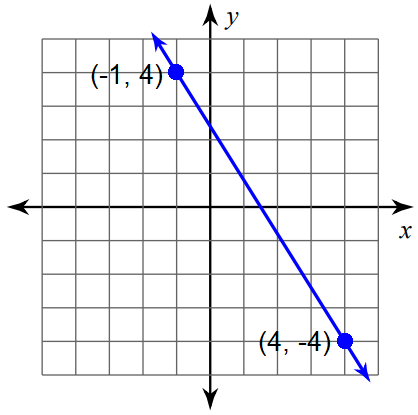
Formula :

Slope  =  (y₂ - y₁) / (x₂ - x₁)

Substitute (x₁, y₁) = (-1, 4) and (x₂, y₂) = (4, -4). 

Slope  =  (-4 - 4) / [4 - (-1)]

Slope  =  -8 / [4 + 1]

Slope  =  -8/5

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.