FIND THE SECOND PARTIAL DERIVATIVES OF THE FUNCTION

Problem 1 :

Let

w(x, y, z) = 1/√(x²+y²+z²), (x, y, z) ≠ (0, 0, 0).

Show that (∂²w/∂x²) + (∂²w/∂y²) + (∂²w/∂z²)

Solution :

Given :

w(x, y, z) = 1/√(x²+y²+z²)

∂w/dx  =  -1/2(x²+y²+z²)^(3/2)(2x)

∂w/dx  =  -x/(x²+y²+z²)^(3/2)

u = -x and v = (x²+y²+z²)^(3/2)

u' = -1 and v' = (3/2)(x²+y²+z²)^1/2 (2x)

v' = 3x(x²+y²+z²)^1/2

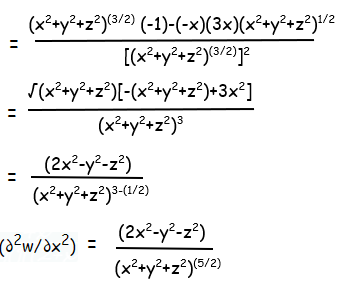
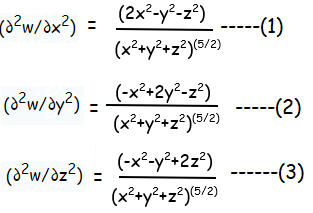
(1) + (2) + (3)

=  (2x²-y²-z²-x²+2y²-z²-x²-y²+2z²)/(x²+y²+z²)^5/2

=  0

Problem 2 :

If V(x, y) = e^x(x cos y - y sin y), then prove that 

∂²w/∂x²  = ∂²w/∂y²

Solution :

Differentiating with respect to x.

∂w/∂x  =  e^x(cos y - 0) + (x cos y - y sin y)e^x

∂w/∂x =  e^x [cos y + x cos y - y sin y]

Differentiate with respect to x.

∂²w/∂x² =  e^x [0 + x (-sin y) + cos y (1) - 0]

∂²w/∂x² =  e^x [-x sin y + cos y] ----(1)

Differentiating with respect to y.

∂w/∂y  =  e^x(-xsiny - [y(cosy) + sin y (1)] )

∂w/∂y =  e^x [-xsiny - ycosy + sin y] 

Differentiate with respect to x.

∂w/∂y =  e^x [-xsiny - ycosy + sin y] 

∂²w/∂y² =  e^x [-xcosy -y(sin y) + cosy(1)+ + cos y

0 + x (-sin y) + cos y (1) - 0]

∂²w/∂x² =  e^x [-x sin y + cos y] ----(2)

(1)  =  (2)

Problem 3 :

If w(x, y) = xy + sin(xy) , then prove that

∂²w/∂y∂x  = ∂²w/∂x∂y

Solution :

Differentiating with respect to y. 

∂w/∂y = x(1) + cos(xy)(x) 

∂w/∂y = x + xcos(xy)

∂w/∂y = x[1 + cos(xy)]

Differentiating with respect to x. 

∂²w/∂y∂x  =  x[0-sin(xy)(y)]+[1 + cos(xy)](1)

∂²w/∂y∂x  =  -xysin(xy) + 1 + cos(xy)

∂²w/∂y∂x  =  1 + cos(xy) -xysin(xy) ----(1)

Differentiating with respect to x. 

Given : w(x, y) = xy + sin(xy)

∂w/∂x = y + cos(xy)(y) 

∂w/∂x = y + ycos(xy)

∂w/∂x = y[1+cos(xy)]

Differentiating with respect to y. 

∂²w/∂x∂y  =  y[0-sin(xy)(x)]+[1 + cos(xy)](1)

∂²w/∂x∂y  =  -xysin(xy) + 1 + cos(xy) ----(2)

(1)  =  (2)

∂²w/∂x∂y  =  1 + cos(xy) -xysin(xy)

Problem 4 :

If V(x, y, z)  =  x³+y³+z³+3xyz, show that 

∂²v/∂y∂z  = ∂²v/∂z∂y

Solution :

Given : V(x, y, z)  =  x³+y³+z³+3xyz

∂v/∂y = 0+3y²+0+3xz

∂v/∂y = 3y²+3xz

∂²v/∂y∂z = 0+3x(1)

∂²v/∂y∂z = 3x  ------(1)

Given : V(x, y, z)  =  x³+y³+z³+3xyz

∂v/∂z = 0+0+3z²+0+3xy

∂v/∂z = 3z²+3xy

∂²v/∂z∂y = 0+3x(1)

∂²v/∂y∂z = 3x -----(2)

(1)  =  (2)

Problem 5 :

A firm produces two types of calculators each week, x number of type A and y number of type B . The weekly revenue and cost functions (in rupees) are

R(x, y) = 80x + 90y + 0.04xy − 0.05x² − 0.05y² and

C(x, y) = 8x + 6y + 2000 respectively.

(i) Find the profit function P(x, y) ,

(ii) Find ∂P/∂x (1200, 1800) and ∂P/∂y (1200, 1800) and interpret these results.

Solution :

To find profit function, we will subtract cost function from revenue function.

P(x, y) = R(x, y) - C(x, y)

= (80x + 90y + 0.04xy − 0.05x² − 0.05y²)-(8x + 6y + 2000)

P(x, y) = (72x + 84y + 0.04xy − 0.05x² − 0.05y²- 2000)

∂P/∂x = 72+0.04y−0.1x

∂P/∂x at (1200, 1800) = 72+0.04(1800)−0.1(1200)

=  72+72-120

=  24

The profit increases.

∂P/∂y = 84+0.04x-0.1y

∂P/∂x at (1200, 1800) = 84+0.04(1200)-0.1(1800)

=  84+48-180

= 132-144

= -48

The profit decreases.

Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.