FIND THE PRODUCT OF RATIONAL EXPRESSIONS
How to multiply the rational expressions ?
If A/B and C/D are rational expressions and B and D are non-zero then,
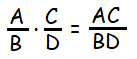
Step 1 :
If the given two rational expressions are based multiplied, we have to multiply the numerator and numerator and multiply the denominator by the denominator.
Step 2 :
If it is possible do factoring and using algebraic identities find factors and simplify.
Step 3 :
After cancelling as much as possible, the left overs are answer.
Note :
Sometimes it may be necessary to use factorization and algebraic identities.
Problem 1 :
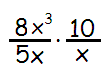
Solution :
Multiply numerators and denominators.
= (8x3/5x) ⋅ (10/x)
Simplifying 10 and 5, we get
= (8x3/5x) ⋅ (2/x)
= 16x
Problem 2 :
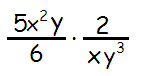
Solution :
Multiply numerators and denominators.
= (5x2 y/6) ⋅ (2 / xy3)
= (5x2 y/6) ⋅ (2 / xy3)
= 5x/3y2
Problem 3 :
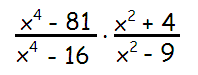
Solution :
x4 - 81 = x4 - 34
= (x2)2 - (32)2
= (x2)2 - 92
= (x2 - 9)(x2 + 9)
= (x2 - 32)(x2 + 9)
= (x + 3)(x - 3)(x2 + 9)
x4 - 16 = x4 - 24
= (x2)2 - (22)2
= (x2)2 - 42
= (x2 - 4)(x2 + 4)
= (x2 - 22)(x2 + 4)
= (x + 2)(x - 2)(x2 + 4)
(x4 - 81 / x4 - 16) ⋅ (x2 + 4)/(x2 - 9)
= [(x + 3)(x - 3)(x2 + 9)/(x + 2)(x - 2)(x2 + 4)] ⋅[ (x2 + 4)/(x2 - 9)]
= (x2 + 9)/(x + 2)(x - 2)
Problem 4 :
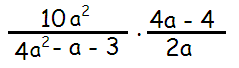
Solution :
4a2 - a - 3 = 4a2 - 4a + 3a - 3
= 4a(a - 1) + 3(a - 1)
= (4a + 3)(a - 1)
4a - 4 = 4(a - 1)
[10a2 / 4a2 - a - 3] ⋅ [(4a - 4) / 2a]
= [10a2 / (4a + 3)(a - 1)] ⋅ [4(a - 1) / 2a]
= 5a(4)/(4a + 3)
= 20a / (4 a + 3)
Problem 5 :
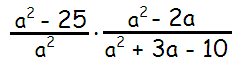
Solution :
a2 - 25 = a2 - 52
= (a + 5)(a - 5)
a2 - 2a = a(a - 2)
a2 + 3a - 10 = a2 + 5a - 2a - 10
= a(a + 5) - 2(a + 5)
= (a + 5)(a - 2)
[a2 - 25 / a2] ⋅ [a2 - 2a / (a2 + 3a - 10)]
= [(a + 5)(a - 5) / a2] ⋅ [a(a - 2)/(a + 5)(a - 2)]
After cancelling common factors, we get
= (a - 5)/a
Problem 6 :
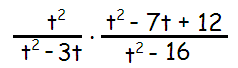
Solution :
[(t2) / (t2 - 3t)] ⋅ [(t2 - 7t + 12) / (t2 - 16)]
t2 - 3t = t(t - 3)
t2 - 7t + 12 = t2 - 4t - 3t + 12
= t(t - 4) - 3(t - 4)
= (t - 3)(t - 4)
t2 - 16 =