FIND THE MISSING VALUE IN MATRICES RANK METHOD

Question 1 :

Find the value of k for which the equations kx − 2y + z =1, x − 2ky + z = −2, x − 2y + kz =1 have

(i) no solution (ii) unique solution (iii) infinitely many solution

Solution :

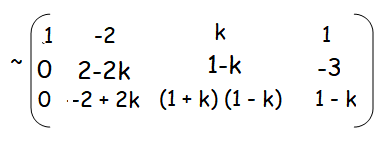
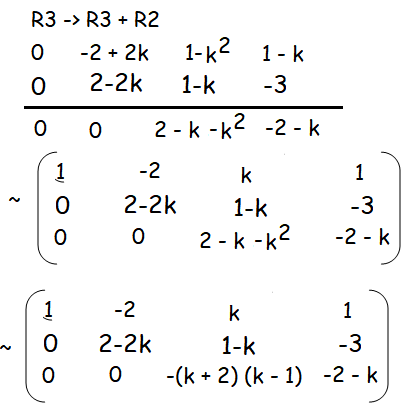
(i) no solution

If k = 1, then

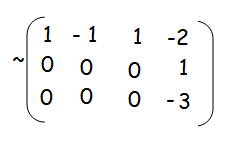
Rank of A is 2, and rank of [A, B] is 3.

Since the ranks are not equal, there is no solution.

(ii) unique solution 

If k  =  -1

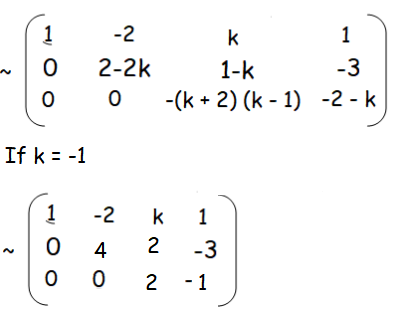
Rank of A is 3, and rank of [A, B] is 3.

Since the ranks are equal, it has unique solution.

(iii) infinitely many solution

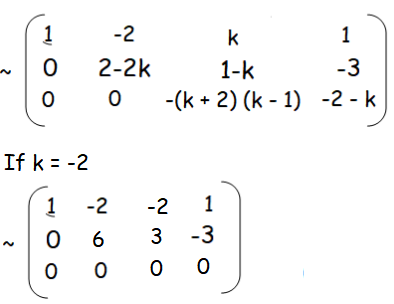
Rank of A is 2, and rank of [A, B] is 2.

Since the ranks are equal and it is less than 3, it has infinitely many solution.

Question 2 :

Investigate the values of λ and m the system of linear equations 2x + 3y + 5z = 9 , 7x + 3y − 5z = 8, 2x + 3y + λz = μ , have

(i) no solution (ii) a unique solution (iii) an infinite number of solutions

Solution :

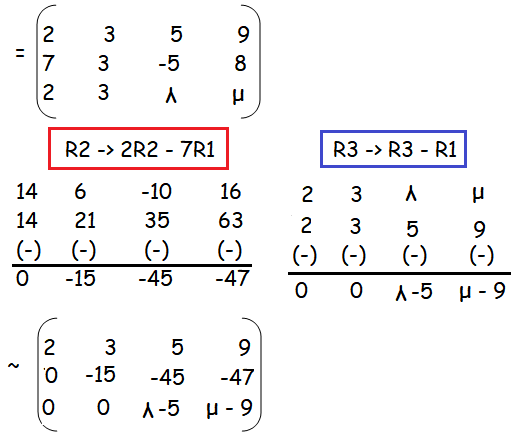
(i)  no solution 

If λ = 5, and  μ ≠ 9

rank of A is 2, rank of [A, B] is 3.

So, it has no solution.

(ii) a unique solution

If λ ≠ 5, and μ = 9

rank of A is 3, rank of [A, B] is 3.

So, it has unique solution.

(iii) an infinite number of solutions

If λ = 5, and μ = 9

rank of A is 2, rank of [A, B] is 2.

So, it has infinite number of solutions.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.