FIND THE MISSING EXPONENT

Example 1 :

Find the missing exponent.

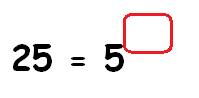
Solution :

Let 'x' be the missing exponent. 

Then, 

25  =  5^x

To get the same base on both sides, write 25 in terms of 5 using exponent. 

5²  =  5^x

Equate the exponents. 

2  =  x

So, the missing exponent is 2.

Example 2 :

Find the missing exponent.

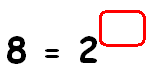
Solution :

Let 'x' be the missing exponent. 

Then, 

8  =  2^x

To get the same base on both sides, write 8 in terms of 2 using exponent. 

2³  =  2^x

Equate the exponents. 

3  =  x

So, the missing exponent is 3.

Example 3 :

Find the missing exponent.

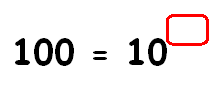
Solution :

Let 'x' be the missing exponent. 

Then, 

100  =  10^x

To get the same base on both sides, write 100 in terms of 10 using exponent. 

10²  =  10^x

Equate the exponents. 

2  =  x

So, the missing exponent is 2.

Example 4 :

Find the missing exponent.

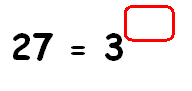
Solution :

Let 'x' be the missing exponent. 

Then, 

27  =  3^x

To get the same base on both sides, write 27 in terms of 3 using exponent. 

3³  =  3^x

Equate the exponents. 

3  =  x

So, the missing exponent is 3.

Example 5 :

Find the missing exponent.

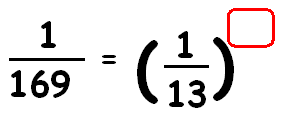
Solution :

Let 'x' be the missing exponent. 

Then, 

1/169  =  (1/13)^x

Write 169 in terms of 13 using exponent. 

1/13²  =  (1/13)^x

13^-2  =  (13^-1)^x

13^-2  =  13^-x

Equate the exponents. 

-2  =  -x

Multiply each side by (-1).

2  =  x

So, the missing exponent is 2.

Example 6 :

Find the missing exponent.

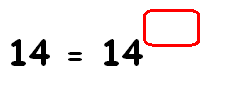
Solution :

Let 'x' be the missing exponent. 

Then, 

14  =  14^x

Already, we have the same on both sides.

14¹  =  14^x

Equate the exponents. 

1  =  x

So, the missing exponent is 1.

Example 7 :

Find the missing exponent.

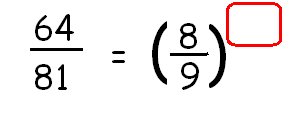
Solution :

Let 'x' be the missing exponent. 

Then, 

64/81  =  (8/9)^x

Write 64 in terms 8 and 81 in terms of 9 using exponent. 

8² / 9²  =  (8/9)^x

(8/ 9)²  =  (8/9)^x

Equate the exponents. 

2  =  x

So, the missing exponent is 2.

Example 8 :

Find the missing exponent.

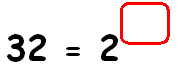
Solution :

Let 'x' be the missing exponent. 

Then, 

32  =  2^x

Write 32 in terms of 2 using exponent. 

2⁵  =  2^x

Equate the exponents. 

5  =  x

So, the missing exponent is 5.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.