FIND THE MIDPOINT OF THE LINE SEGMENT WHOSE ENDPOINTS ARE GIVEN

The mid-point M of the line segment joining the points A(x₁, y₁) and B(x₂ , y₂) is

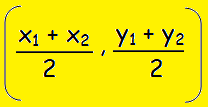
Question 1 :

Find the mid-points of the line segment joining the points

(i) (−2, 3) and (−6,−5)

Solution :

(x₁, y₁) ==>  (-2, 3)

(x₂ , y₂) ==> (-6, -5)

Midpoint  =  (-2 - 6)/2, (3 + (-5))/2

   =  -8/2, -2/2

  =  (-4, -1)

(ii) (8,−2) and (−8,0)

Solution :

(x₁, y₁) ==>  (8, -2)

(x₂ , y₂) ==> (-8, 0)

Midpoint  =  (8 - 8)/2, (-2 + 0)/2

   =  0/2, -2/2

  =  (0, -1)

(iii) (a, b) and (a + 2b, 2a - b)

Solution :

(x₁, y₁) ==>  (a, b)

(x₂ , y₂) ==> (a + 2b, 2a - b)

Midpoint  =  (a + a + 2b)/2, (b + 2a - b)/2

   =  2(a + b)/2, 2a/2

  =  (a + b, 1)

(iv) (1/2, -3/7) and (3/2, -11/7)

Solution :

(x₁, y₁) ==>  (1/2, -3/7)

(x₂ , y₂) ==> (3/2, -11/7)

Midpoint  =  ((1/2) + (3/2))/2, ((-3/7) + (-11/7))/2

 =  ((4/2)/2, ((-14/7)/2)

=  (1, -1)

Question 2 :

The centre of a circle is (−4,2). If one end of the diameter of the circle is (−3,7), then find the other end

Solution :

Midpoint of the diameter =  Center of the circle

Let the other endpoint be (a, b)

Midpoint of (-3, 7) and (a, b) is (-4, 2).

(-3 + a)/2, (7 + b)/2  =  (-4, 2)

By equating the x and y coordinates, we get

Hence the other end is (-5, -3).

Question 3 :

If the mid-point (x, y) of the line joining (3, 4) and (p, 7) lies on 2x + 2y + 1 = 0 , then what will be the value of p?

Solution :

Midpoint of the line segment joining the points (3, 4) and (p, 7)

(3 + p)/2 , (7 + 4)/2  =  (x, y)

(3 + p)/2 , 11/2  =  (x, y)

x  =  (3 + p)/2 and y  =  11/2

Since the midpoint lies on the line 2x + 2y + 1  =  0

2(3 + p)/2 + 2(11/2) + 1  =  0

3 + p + 11 + 1  =  0

p + 15  =  0

p  =  -15

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.