FIND THE MEAN MEDIAN AND MODE FOR EACH SET OF NUMBERS

Mean :

The arithmetic mean of a given numbers is the sum of all observations divided by the number of observations.

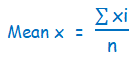
(where ∑x_i is the sum of all observations and n is number of observations)

Median :

The median is the middle value of a given numbers when those values are arranged from ascending to descending order.

Median  =  Middle value

To find the median from the ungrouped numbers, we have to consider if n is odd or even.

If n is even, then using the formula

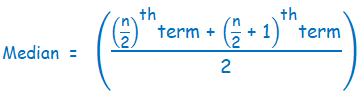
If n is odd, then using the formula

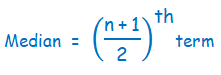
Mode :

The mode is the value that occurs most often in the given numbers.

Find the mean, median, mode of the following set of numbers.

Problem 1 :

24, 31, 12, 38, 12, 15

Solution :

Let us arrange the numbers in ascending order.

12, 12, 15, 24, 31, 38

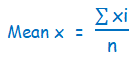
=  (12 + 12 + 15 + 24 + 31 + 38)/6

=  132/6

Mean x  =  22

The number of values  =  6

Which is even,

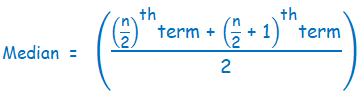
=  ((6/2^th term) + ((6/2 + 1)^th term))/2

=  1/2 (3^th term + 4^th term)

=  1/2 (15 + 24)

=  1/2 (39)

Median  =  19.5

Mode  =  12

So, 12 is repeating the largest number of times.

Problem 2 :

5, 28, 16, 32, 5, 16, 48, 29, 5, 35

Solution :

Let us arrange the numbers in ascending order.

5, 5, 5, 16, 16, 28, 29, 32, 35, 48

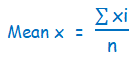
=  (5 + 5 + 5 + 16 + 16 + 28 + 29 + 32 + 35 + 48)/10

=  219/10

Mean x  =  21.9

The number of values  =  10

Which is even,

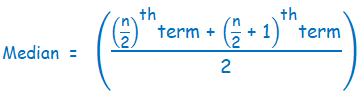
= ((10/2)^th term) + ((10/2 + 1)^th term))/2

=  1/2 (5^th term + (5 + 1)^th term)

=  1/2 (5^th term + 6^th term)

=  1/2 (16 + 28)

 =  1/2 (44)

Median  =  22

Mode  =  5

So, 5 is repeating the largest number of times.

Problem 3 :

53, 13, 34, 41, 26, 61, 34, 13, 69

Solution :

Let us arrange the numbers in ascending order.

13, 13, 26, 34, 34, 41, 53, 61, 69

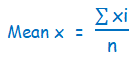
=  (13 + 13 + 26 + 34 + 34 + 41 + 53 + 61 + 69)/9

=  344/9

Mean x =  38.22

The number of values  =  9

Which is odd,

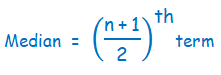
=  ((9 + 1)/2)^th term

=  ((10/2)^th) term

=  (5^th term)

Median  =  34

Mode  =  13 and 34

So, 13 and 34 are repeating the largest number of times.

Problem 4 :

85, 58, 72, 85, 46, 93

Solution :

Let us arrange the numbers in ascending order.

46, 58, 72, 85, 85, 93

Mean  =  (46 + 58 + 72 + 85 + 85 + 93)/6

=  439/6

Mean x =  73.2

The number of values  =  6

Which is even,

Median  = ((6/2)^th term) + ((6/2 + 1)^th term))/2

=  1/2 (3^th term + (3 + 1)^th term)

=  1/2 (3^th term + 4^th term)

=  1/2 (72 + 85)

=  1/2 (157)

Median  =  78.5

Mode  =  85

So, 85 is repeating the largest number of times.

Problem 5 :

92, 63, 22, 80, 63, 71, 44, 35

Solution :

Let us arrange the numbers in ascending order.

22, 35, 44, 63, 63, 71, 80, 92

Mean  =  (22 + 35 + 44 + 63 + 63 + 71 + 80 + 92)/8

=  470/8

Mean x =  58.75

The number of values  =  8

Which is even,

Median  = ((8/2)^th term) + ((8/2 + 1)^th term))/2

=  1/2 (4^th term + (4 + 1)^th term)

=  1/2 (4^th term + 5^th term)

=  1/2 (63 + 63)

=  1/2 (126)

Median  =  63

Mode  =  63

So, 63 is repeating the largest number of times.

Problem 6 :

39, 82, 74, 96, 64, 52, 74

Solution :

Let us arrange the numbers in ascending order.

39, 52, 64, 74, 74, 82, 96

Mean  =  (39 + 52 + 64 + 74 + 74 + 82 + 96)/7

=  481/7

Mean x =  68.71

The number of values  =  7

Which is odd,

Median  =  ((7 + 1)/2)^th term

=  ((8/2)^th) term

=  (4^th term)

Median =  74

Mode  =  74

So, 74 is repeating the largest number of times.

Problem 7 :

72, 43, 15, 66, 32, 72, 52, 19, 28, 81

Solution :

Let us arrange the numbers in ascending order.

15, 19, 28, 32, 43, 52, 66, 72, 72, 81

Mean  =  (15 + 19 + 28 + 32 + 43 + 52 + 66 + 72 + 72 + 81)/10

=  480/10

Mean x  =   48

The number of values  =  10

Which is even,

Median  = ((10/2)^th term) + ((10/2 + 1)^th term))/2

=  1/2 (5^th term + 6^th term)

=  1/2 (43 + 52)

 =  1/2 (95)

Median  =  47.5

Mode  =  72

So, 72 is repeating the largest number of times.

Problem 8 :

40, 90, 36, 68, 90, 11, 88, 54

Solution :

Let us arrange the numbers in ascending order.

11, 36, 40, 54, 68, 88, 90, 90

=  (11 + 36 + 40 + 54 + 68 + 88 + 90 + 90)/8

=  477/8

Mean x  =  59.62

The number of values  =  8

Which is even,

= ((8/2)^th term) + ((8/2 + 1)^th term))/2

=  1/2 (4^th term + (4 + 1)^th term)

=  1/2 (4^th term + 5^th term)

=  1/2 (54 + 68)

=  1/2 (122)

Median =  61

Mode  =  90

So, 90 is repeating the largest number of times.

Problem 9 :

12, 46, 32, 18, 26, 41, 46

Solution :

Let us arrange the numbers in ascending order.

12, 18, 26, 32, 41, 46, 46

=  (12 + 18 + 26 + 32 + 41 + 46 + 46)/7

= 221/7

Mean x =  31.6

The number of values  =  7

Which is odd,

Median  =  ((7 + 1)/2)^th term

=  ((8/2)^th) term

=  (4^th term)

Median  =  32

Mode  =  46

So, 46 is repeating the largest number of times.

Problem 10 :

63, 40, 51, 70, 36, 21, 51, 28, 19

Solution :

Let us arrange the numbers in ascending order.

19, 21, 28, 36, 40, 51 , 51, 63, 70

=  (19 + 21 + 28 + 36 + 40 + 51 + 51 + 63 + 70)/9

=  379/9

Mean x =  42.11

The number of values  =  9

Which is odd,

=  ((9 + 1)/2)^th term

=  ((10/2)^th) term

=  (5^th term)

Median  =  40

Mode  =  51

So, 51 is repeating the largest number of times.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.