FIND THE MAGNITUDE AND DIRECTION COSINES OF GIVEN VECTORS

Question 1 :

If 

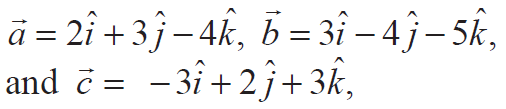
find the magnitude and direction cosines of

(i) a vector + b vector + c vector

(ii)  3a vector - 2b vector + 5c vector

Solution :

(i) a vector + b vector + c vector 

  =  (2i + 3j - 4k) + (3i - 4j - 5k) + (-3i + 2j + 3k)

  =  (2i + 3i - 3i) + (3j - 4j + 2j) + (-4k - 5k + 3k)

  =  (2i + j - 6k) vector

|a vector + b vector + c vector|   =  √2² + 1² + (-6)²

  =  √(4+1+36)  =  √41

Direction cosines are (x/r, y/r, z/r)

That is, (2/√41, 1/√41, -6/√41)

Hence magnitude and direction cosines are √41 and (2/√41, 1/√41, -6/√41) respectively.

(ii)  3a vector - 2b vector + 5c vector

Solution :

3a vector  =  3(2i+3j-4k)-2(3i-4j-5k)+5(-3i+2j+3k)

  =  (6-6-15)i + (9+8+10)j+(-12+10+15)k

  =  -15i + 27j + 13k

|3a vector - 2b vector + 5c vector  =  √(-15)² + 27² + 13²

  =  √225 + 729 + 169

  =  √1123

Direction cosines are (x/r, y/r, z/r)

That is, (15/√1123, 27/√1123, 13/√1123)

Hence magnitude and direction cosines are √1123 and (15/√1123, 27/√1123, 13/√1123) respectively.

Question 2 :

The position vectors of the vertices of a triangle are i+2j +3k; 3i − 4j + 5k and − 2i+ 3j − 7k . Find the perimeter of the triangle (Given in vectors)

Solution :

To find the perimeter of the triangle, we have find the sum of all sides.

OA vector  =  i + 2j + 3k

OB vector  =  3i − 4j + 5k 

OC vector  =   -2i+ 3j − 7k

AB  =  OB - OA

  =  (3i − 4j + 5k) - (i + 2j + 3k)

AB vector  =  2i - 6j + 2k

|AB vector|  =  √2² + (-6)² + 2²

=  √(4+36+4)  =  √44  ----(1)

BC  =  OC - OB

  =  (-2i+ 3j − 7k) - (3i − 4j + 5k)

BC vector  =  -5i + 7j - 12k

|AB vector|  =  √(-5)² + 7² + (-12)²

=  √(25 + 49 + 144)  =  √218  ----(2)

CA  =  OA - OC

  =  (i + 2j + 3k) - (-2i+ 3j − 7k)

CA vector  =  3i - j + 10k

|AB vector|  =  √3² + (-1)² + 10²

=  √(9 + 1 + 100)  =  √110  ----(3)

Perimeter of triangle  =  √44 + √218 + √110

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.