MAJOR AXIS AND MINOR AXIS OF ELLIPSE

Standard equation of an ellipse (symmetric about x-axis) :

Here, the center of the ellipse is (h, k).

When the center of the ellipse is origin (0, 0), then the above equation becomes as shown below.

Here a > b.

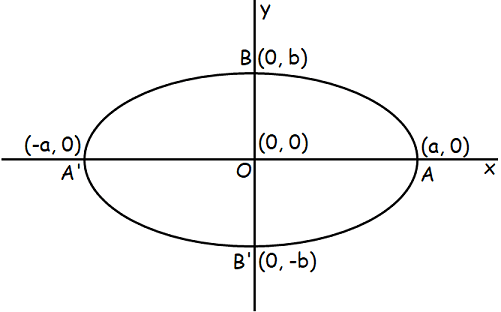
Major Axis :

The line segment AA′ is called the major axis and the length of the major axis is 2a. The equation of the major axis is y = 0.

Minor Axis :

The line segment BB′ is called the minor axis and the length of minor axis is 2b. Equation of the minor axis is x = 0.

Standard equation of an ellipse (symmetric about y-axis) :

Here, the center of the ellipse is (h, k).

When the center of the ellipse is origin (0, 0), then the above equation becomes as shown below.

Here a > b.

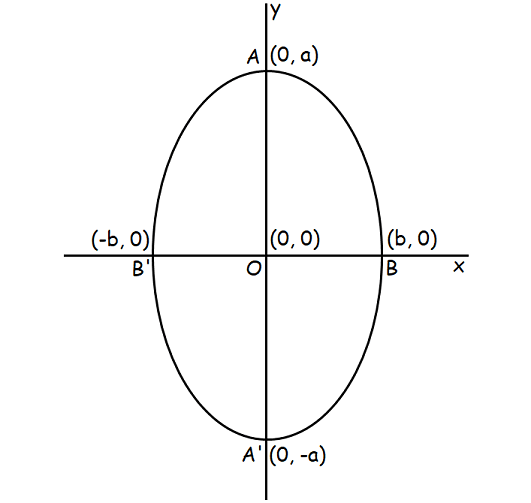
Length of the major axis = AA' = 2a.

Equation of the major axis is x = 0.

Length of the minor axis = BB' = 2b.

Equation of the minor axis is y = 0.

Note that the length of major axis is always greater than minor axis.

Find the equations and lengths of major and minor axes of the following ellipses.

Example 1 :

Solution :

The major axis is along x-axis and the minor axis is along y-axis.

Equation of major axis : y = 0.

Equation of minor axis : x = 0.

a² = 9 ----> a = 3

b² = 4 ----> b = 2

Length of major axis :

= 2a

= 2(3)

= 6

Length of minor axis :

= 2b

= 2(2)

= 4

Example 2 :

4x² + 3y² = 12

Solution :

4x² + 3y² = 12

Divide both sides by 12.

The major axis is along y-axis and the minor axis is along x-axis.

Equation of major axis : x = 0.

Equation of minor axis : y = 0.

a² = 4 ----> a = 2

b² = 3 ----> b = √3

Length of major axis :

= 2a

= 2(2)

= 4

Length of minor axis :

= 2b

= 2√3

Example 3 :

6x² + 9y² + 12x - 36y - 12 = 0

Solution :

The given equation of ellipse is not in standard form. Convert it to standard form.

6x² + 9y² + 12x - 36y - 12 = 0

6x² + 12x + 9y² - 36y - 12 = 0

6(x² + 2x) + 9(y² - 4y) - 12 = 0

6[x² + 2x(1) + 1² - 1²] + 9[y² - 2y(2) + 2² - 2²] - 12 = 0

6[(x + 1)² - 1] + 9[(y - 2)² - 4] - 12 = 0

6(x + 1)² - 6 + 9(y - 2)² - 36 - 12 = 0

6(x + 1)² + 9(y - 2)² - 54 = 0

6(x + 1)² + 9(y - 2)² = 54

Divide both sides by 54.

Let X = x - 1 and Y = y - 2.

Clearly the major axis is along X-axis and the minor axis is along Y-axis.

Equation of the major axis :

Y = 0

y - 2 = 0

y = 2

Equation of the minor axis :

X = 0

x + 1 = 0

x = -1

Here,

a² = 9 ----> a = 3

b² = 6 ----> b = √6

Length of major axis :

= 2a

= 2(3)

= 6

Length of minor axis :

= 2b

= 2√6

Example 4 :

36x² - 72x + 4y² + 32y - 44 = 0

Solution :

The given equation of ellipse is not in standard form. Convert it to standard form.

36x² - 72x + 4y² + 32y - 44 = 0

36(x² - 2x) + 4(y² + 8y) - 44 = 0

36[x² - 2x(1) + 1² - 1²] + 4[y²+ 2y(4) + 4² - 4²] - 44 = 0

36[(x - 1)²- 1] + 4[(y + 4)²- 16] - 44 = 0

36(x - 1)² - 36 + 4(y + 4)² - 64 - 44 = 0

36(x - 1)²+ 4(y + 4)² - 144 = 0

36(x - 1)²+ 4(y + 4)² = 144

Divide both sides by 144.

Let X = x - 1 and Y = y + 4. 

Clearly the major axis is along Y-axis and the minor axis is along X-axis.

Equation of the major axis :

X = 0

x - 1 = 0

x = 1

Equation of the minor axis :

Y = 0

y + 4 = 0

y = -4

Here,

a² = 36 ----> a = 6

b² = 4 ----> b = 2

Length of major axis :

= 2a

= 2(6)

= 12

Length of minor axis :

= 2b

= 2(2)

= 4

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.