FIND THE EXACT VALUE OF TRIGONOMETRIC FUNCTIONS
To find the exact value of trigonometric ratios, we should be aware of special right triangles and reference angles.
45° - 45° - 90° Triangle Theorem :
In a 45° - 45° - 90° triangle, the hypotenuse is √2 times as long as each leg.
It has been illustrated in the diagram shown below.
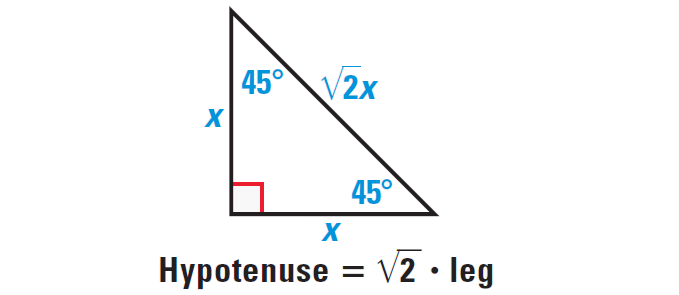
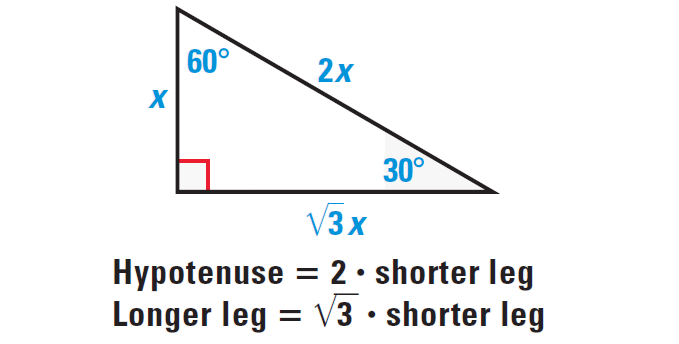
30° - 60° - 90° Triangle Theorem :
In a 30° - 60° - 90° triangle, the hypotenuse is twice as long as the shorter leg, and the longer leg is √3 times as long as the shorter leg.
It has been illustrated in the diagram shown below.
Find the exact value of the following
Example 1 :
sin π/6
Solution :
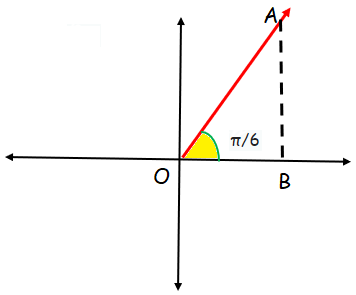
The triangle drawn above comes under 30-60-90 special right triangle.
<OAB = 30, < AOB = 60 and <OBA = 90
If OB(shorter leg) = x, then OA(hypotenuse) = 2x
If OB(shorter leg) = 1, then OA(hypotenuse) = 2
Using ASTC formula,
AB = √3(1) ==> √3
sin θ = Opposite side/hypotenuse
sin π/6 = √3/2
Example 2 :
tan π/4
Solution :
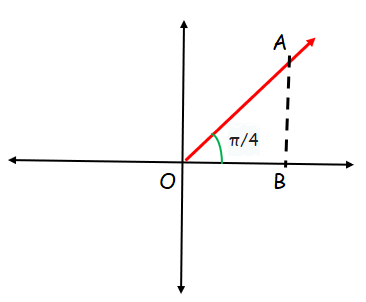
The triangle drawn above comes under 45-45-90 special right triangle.
<OAB = 45, < AOB = 45 and <OBA = 90
If AB = x, then OA(hypotenuse) = √2x
If AB = 1, then OB = 1
tan θ = Opposite side/adjacent side
tan π/4 = 1/1
tan π/4 = 1
Example 3 :
cos 2π/3
Solution :
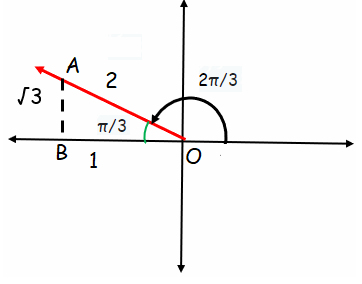
cos 2π/3 = cos (π - π/3)
Using ASTC formula, the 2nd quadrant will have
= -cos (π/3)
Accordingly 30-60-90 special right triangle
cos (π/3) = 1/2
Example 4 :
sin 2π/3
Solution :
sin 2π/3 = sin (π - π/3)
Using ASTC formula, the 2nd quadrant will have
= sin (π/3)
Accordingly 30-60-90 special right triangle
sin (π/3) = √3/2
Example 5 :
sin (-π/6)
Solution :
sin (-π/6) = -sin (π/6)
= -1/2
Example 6 :
sin (7π/4)
Solution :
sin (7π/4) = sin (2π - 7π/4)
It comes in the fourth quadrant. Using ASTC formula
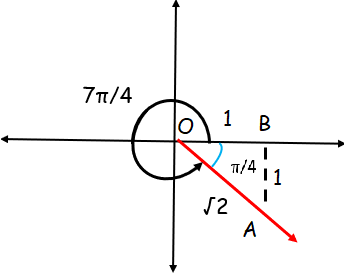
= sin (2π - 7π/4)
= -sin (π/4)
= -1/√2
Example 7 :
cos (-150)
Solution :
cos (-150) = cos 150
The given angle measure 150 lies in the second quadrant, then its reference angle will be 180 - θ
= cos (180 - 150)
= -cos 30
= -√3/2
Example 8 :
cos (-5π/4)
Solution :
cos (-5π/4) = cos (5π/4)
Using ASTC formula, the given angle measure 5π/4 lies in the third quadrant.
Reference angle is θ - π
= (5π/4) - π
= π/4
cos (5π/4) = -cos (π/4)
= - √2/2
Example 9 :
tan (-4π/3)
Solution :
tan (-4π/3) = - tan (4π/3)
Using ASTC formula, the given angle measure 4π/3 lies in the third quadrant.
Reference angle is θ - π
= (4π/3) - π
= π/3
tan (-4π/3) = -tan (π/3)
= - √3
Example 10 :
cos (-7π/3)
Solution :
cos (-7π/3) = cos (7π/3)
Since it is more than 360, we write the given angle measure as sum of 360.
6π/3 + π/3 = 2π + π/3
Using ASTC formula, the given angle measure π/3 lies in the third quadrant.
cos (-7π/3) = cos (π/3)
= 1/2
Example 11 :
sec (-60)
Solution :
sec (-60) = sec 60
= 1/cos 60
= 1/(1/2)
= 2
Example 12 :
cos (-330)
Solution :
cos (-330) = cos 330
The angle lies in the fourth quadrant. The reference angle 360 - θ
360 - 330 = 30
Using ASTC, it lies in the fourth quadrant, for cosine and its reciprocal sec we have positive.
cos 330 = cos 30
= √3/2
Example 13 :
cot (90)
Solution :
cot (90) = 1/tan 90
= 1/∞
= 0
Example 14 :
cot (5π/6)
Solution :
cot (5π/6)
The angle measure lies in the second quadrant, using ASTC the sign of the we use is negative.
Refence angle = π - θ
= π - 5π/6
= π/6
cot (5π/6) = cot (π/6)
= 1/tan (π/6)
= 1/(1/√3)
= √3
Example 15 :
sec (-7π/4)
Solution :
sec (-7π/4) = sec (7π/4)
The angle measure lies in the fourth quadrant, using ASTC the sign of the we use is positive.
Refence angle = 2π - θ
= 2π - 7π/4
= π/4
sec (7π/4) = 1/cos (π/4)
= 1/(√2/2)
= 2/√2
Example 16 :
tan (-240)
Solution :
tan (-240) = -tan 240
The angle measure lies in the third quadrant, using ASTC the sign of the we use is positive.
Refence angle = θ - 180
= 240 - 180
= 60
tan (-240) = -tan60
= -√3
Example 16 :
csc (-11π/6)
Solution :
csc (-11π/6) = -csc (11