FIND THE EQUATION OF THE TANGENT TO THE CIRCLE AT THE POINT

A tangent to a circle is a straight line which intersects (touches) the circle in exactly one point.

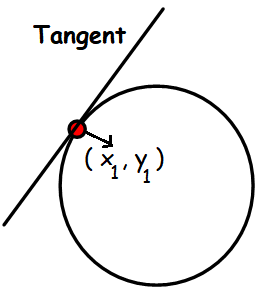
To find the equation of tangent at the given point, we have to replace the following

x²  =  xx₁, y²  =  yy₁, x = (x + x₁)/2, y  =  (y + y₁)/2

Let us look into some examples to understand the above concept.

Example 1 :

Find the equation of the tangent to x² + y² − 2x − 10y + 1 = 0 at (− 3, 2)

Solution :

Equation of tangent at (x₁, y₁) :

xx₁ + yy₁ − 2((x + x₁)/2) − 10((y + y₁)/2) + 1 = 0 

xx₁ + yy₁ − (x + x₁) − 5(y + y₁)  + 1 = 0 

at the point (-3, 2)

x(-3) + y(2) − (x - 3) − 5(y + 2)  + 1 = 0 

-3x + 2y - x + 3 - 5y - 10 + 1  =  0

  -4x - 3y - 6  =  0

Multiply by (-) on both sides

4x + 3y + 6  =  0

Let us look into the next example on "Find the equation of the tangent to the circle at the point".

Example 2 :

Find the equation of the tangent to the circle x² + y² − 4x + 2y − 21 = 0 at (1, 4)

Solution :

Equation of tangent at (x₁, y₁) :

xx₁ + yy₁ - 4((x + x₁)/2) + 2((y + y₁)/2) - 21  =  0 

xx₁ + yy₁ − 2(x + x₁) + (y + y₁)  - 21 = 0 

at the point (1, 4)

x(1) + y(4) − 2(x + 1) + (y + 4)  - 21 = 0 

x + 4y - 2x - 2 + y + 4 - 21  =  0

-x + 5y - 23 + 4  =  0

x - 5y - 19  =  0

Example 3 :

Find the equation of the tangent to the circle x² + y² = 16 which are

(i) perpendicular and

(ii) parallel to the line x + y = 8

Solution :

Equation of tangent to the circle will be in the form

y = mx + a √(1 + m²)

here "m" stands for slope of the tangent,

Since the tangent line drawn to the circle x² + y² = 16 is perpendicular to the line x + y = 8, the product of slopes will be equal to -1.

m  =  -1/(-1)  ==>  1

y = mx + a √(1 + m²)

y  =  1x + 4 √(1 + 1²)

y  =  x + 4 √2

x - y + 4 √2  =  0

Hence the equation of the tangent perpendicular to the given line is x - y + 4 √2  =  0.

(ii)  Since the tangent line drawn to the circle x² + y² = 16 is parallel to the line x + y = 8, the slopes of the tangent line and given line will be equal.

m  =  -1/1  =  -1

x² + y² = 16 

a²  =  16 ==> a = 4

y = mx + a √(1 + m²)

y  =  -1x + 4 √(1 + (-1)²)

y  =  -x + 4 √2

x + y - 4 √2  =  0

Hence the equation of the tangent parallel to the given line is x + y - 4 √2  =  0.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.