FIND THE EQUATION OF THE LINE IN THE NEW POSITION

Example 1 :

If the line joining two points A(2,0) and B(3,1) is rotated about A in anticlockwise direction through an angle of 15°, then find the equation of the line in new position.

Solution :

Let us represent the given information in a picture.

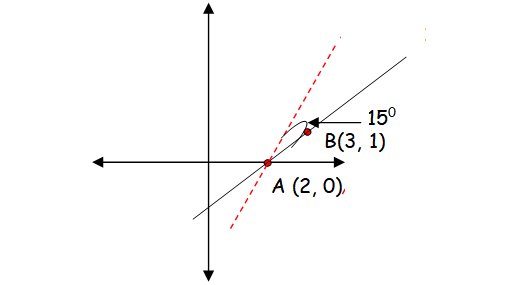
Let A (2, 0) and B (3, 1) be the given points.

Slope of PQ  = (y₂ − y₁) / (x₂ − x₁) 

  =  (1 - 0) / (3 - 2)

  = 1 ⇒ the angle of inclination of

the line AB = tan−1(1) = π/4  = 45^◦

The slope of the line in new position is

m = tan(45^◦ + 15^◦)

Slope = tan(60^◦) = (√3)

Equation of the straight line passing through (2, 0) and with the slope √3 is

y − 0  =  2 (x − √3)

2x − y + 2√3  =  0

Example 2 :

A ray of light coming from the point (1, 2) is reflected at a point A on the x-axis and it passes through the point (5,3). Find the co-ordinates of the point A.

Solution :

Let us represent the given details in a rough diagram.

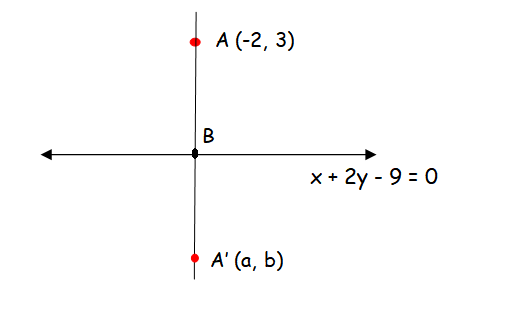
The reflection point of A is A'. Its coordinate will be (1, -2).

Equation of A'B :

A'(1, -2)  B (5, 3)

(y - y₁) / (y₂ - y₁)  =  (x - x₁)/(x₂ - x₁)

(y - 3) / (3 + 2)  =  (x - 5)/(5 - 1)

(y - 3) / 5  =  (x - 5)/4

4 (y - 3)  =  5 (x - 5)

4y - 12  =  5x - 25

5x - 4y - 25 + 12  =  0

5x - 4y - 13  =  0

The required point (x, 0) lies on the line A'B

5x - 4(0) - 13  =  0

5x - 13  =  0

5x  =  13

x  =  13/5

Hence the required point is (13/5, 0).

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.