FIND THE DISTANCE BETWEEN A GIVEN POINT AND LINE
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
The distance from the point to the line is the distance from the point to the foot of the perpendicular.
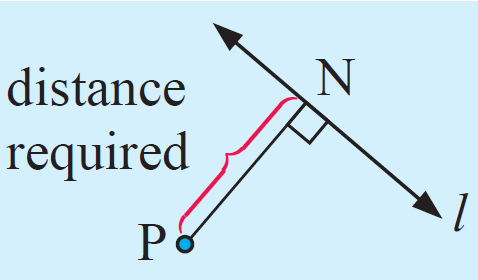
To find out the foot of perpendicular(N) drawn from the point P, we follow the steps given below.
Step 1 :
Since the lines are perpendicular, the product of their slopes will be equal to -1.
Step 2 :
Slope of perpendicular line = -1/Slope of given line
Step 3 :
Find the equation using the given point and slope what we have derived from step 2.
Step 4 :
Solve the system of equations to find point of intersection.
Step 5 :
Find the distance between two points.
Distance formula = √(x2–x1)2 + (y2–y1)2
Find the distance from :
Example 1 :
(8, - 5) to y = - 2x – 4
Solution :
Step 1 :
y = - 2x – 4 -----(1)
By comparing the given equation with slope intercept form (y = mx + b)
slope (m) = - 2
Step 2 :
slope of perpendicular line = 1/2
Step 3 :
Find the equation of the perpendicular line passes through (8, - 5)
(8, - 5)---->(x1, y1)
m = 1/2
(y – y1) = m(x – x1)
(y + 5) = 1/2(x - 8)
2(y + 5) = x – 8
2y = x – 8 -10
2y = x – 18 -----(2)
Step 4 :
Find the point of intersection of two lines,
By applying (1) in (2), we get
2(- 2x – 4) = x – 18
- 4x – 8 = x – 18
x = 2
2y = 2 – 18
2y = - 16
y = - 8
Foot of perpendicular is (2, -8)
Step 5 :
Distance between two points :
= √(2 - 8)2 + (- 8 + 5)2
= 3√5 units.
So, the required distance is 3√5 units.
Example 2 :
(- 10, 9) to y = - 4x + 3
Solution :
y = - 4x + 3 -----(1)
slope (m) = - 4
slope of perpendicular line = 1/4
Equation of perpendicular line :
(- 10, 9)---->(x1, y1)
m = 1/4
(y – y1) = m(x – x1)
(y - 9) = 1/4(x + 10)
4y – 36 = x + 10
4y = x + 46 -----(2)
By applying (1) in (2), we get
4(- 4x + 3) = x + 46
-16x + 12 = x + 46
x = - 2
4y = x + 46
4y = - 2 + 46
y = 44/4
y = 11
Foot of perpendicular is (- 2, 11)
Distance between two points :
= √(- 2 + 10)2 + (11 - 9)2
= 2√17 units.
So, the required distance is 2√17 units.
Example 3 :
(- 2, 8) to 3x – y = 6
Solution :
- y = - 3x + 6
y = 3x – 6 -----(1)
slope (m) = 3
slope of perpendicular line = - 1/3
Equation of perpendicular line :
(y – y1) = m(x – x1)
(y - 8) = - 1/3(x + 2)
3y – 24 = - x – 2
3y = - x + 22 -----(2)
By applying (1) in (2), we get
3(3x – 6) = - x + 22
9x – 18 = - x + 22
x = 4
3y = - x + 22
3y = - 4 + 22
y = 6
Foot of perpendicular is (4, 6)
Distance between two points :
= √(4 + 2)2 + (6 - 8)2
= 2√10 units.
So, the required distance is 2√10 units.
Example 4 :
(1, 7) to 4x – 3y = 8
Solution :
4x – 3y = 8
- 3y = - 4x + 8
y = 4/3x – 8/3 -----(1)
slope (m) = 4/3
slope of perpendicular line = - 1/(4/3)
= - 3/4
Equation of perpendicular line :
(y – y1) = m(x – x1)
(y - 7) = - 3/4(x - 1)
4y – 28 = - 3x + 3
4y = - 3x + 31 -----(2)
By applying (1) in (2), we get
4(4/3x – 8/3) = - 3x + 31
16/3x – 32/3 = - 3x + 31
x = 5
4y = - 3x + 31
4y = - 3(5) + 31
y = 4
Foot of perpendicular is (5, 4)
Distance between two points :
= √(5 - 1)2 + (4 - 7)2
= 5 units
So, the required distance is 5 units.
|
3(3x–5) = -x-5 9x-15 = -x-5 x = 1 |
3y = -1-5 3y = -6 y = -2 |
Foot of perpendicular is (1, -2).
Step 5 :
Distance between two points :
= √(1–7)2 + (-2+4)2
= √40
= 2√10 units.
So, the required distance is 2√10 units.
Example 2 :
(-6, 0) to y = 3–2x
Solution :
y = 3–2x ----(1)
By comparing the given equation with y = mx+b, we come so know slope (m)
Slope (m) = - 2
Slope of perpendicular line = 1/2
Equation of perpendicular line :
(y - 0) = 1/2(x + 6)
2y = x+6 ----(2)
Applying (1) in (2), we get
|
2(3–2x) = x+6 6-4x = x+6 -5x = 0 x = 0 |
2y = 0+6 2y = 6 y = 3 |
So, foot of perpendicular is (0, 3).
Distance between (-6, 0) and (0, 3).
= √(0+6)2 + (3-0)2
= √(36+9)
= √45
= 3√5
units.
So, the required distance is 3√5 units.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
10 Hard SAT Math Questions (Part - 43)
Jan 04, 26 01:38 AM
10 Hard SAT Math Questions (Part - 43) -
90 Degree Clockwise Rotation
Jan 01, 26 06:58 AM
90 Degree Clockwise Rotation - Rule - Examples with step by step explanation -
US Common Core K-12 Curriculum Algebra Solving Systems of Equations
Jan 01, 26 04:51 AM
US Common Core K-12 Curriculum - Algebra : Solving Systems of Linear Equations
