FIND THE DERIVATIVES FROM THE LEFT AND RIGHT AT THE GIVEN POINT

About "Find the Derivatives From the Left and Right at the Given Point"

Find the Derivatives From the Left and Right at the Given Point :

Here we are going to see how to find the derivatives from the left and right at the given point.

Find the Derivatives From the Left and Right at the Given Point - Examples

For a function y = f(x) defined in an open interval (a, b) containing the point x₀, the left hand and right hand derivatives of f at x = h are respectively denoted by f'(h^-) and f'(h⁺)

f'(h^-)  =  lim _{h-> 0}^-[f(x + h) - f(x)] / h

f'(h⁺)  =  lim _{h-> 0}⁺[f(x + h) - f(x)] / h

provided the limits exist.

Question 1 :

Find the derivatives from the left and from the right at x = 1 (if they exist) of the following functions. Are the functions differentiable at x = 1?

(i)  f(x)  =  |x - 1|

Solution :

If the function is differentiable, then

f'(1^-)  =  f'(1⁺)

f'(1^-)  = lim_x->1- [f(x) - f(1)] / (x - 1)

=  lim_x->1- [-(x - 1) - 0]/(x - 1)

=  -1

f'(1⁺)  =  lim_x->1+  [f(x) - f(1)] / (x - 1)

=   lim_x->1+ [(x - 1) - 0]/(x - 1)

=  1

Hence the given function is not differentiable at x = 1.

(ii)  f(x)  =  √(1 - x²)

Solution :

If the function is differentiable, then

f'(1^-)  =  f'(1⁺)

f'(1^-)  =  [f(x) - f(1)] / (x - 1)

=   lim_x->1- [√(1 - x²) - 0]/(x - 1)

=   lim_x->1- [√(1 - x²) - 0]/(1 - x)

=   lim_x->1- -√(1 + x) / √(1 - x)

=  -√2 / 0

=  -∞

Hence the given function is not differentiable at x = 1.

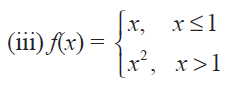
Solution :

If the function is differentiable, then

f'(1^-)  =  f'(1⁺)

f'(1^-)  = lim_x->1- [f(x) - f(1)] / (x - 1)

=  lim_x->1- (x - 1)/(x - 1)

=  1

f'(1⁺)  =  lim_x->1+  [f(x) - f(1)] / (x - 1)

=   lim_x->1+ (x² - 1)/(x - 1)

=  lim_x->1+ (x + 1)(x - 1)/(x - 1)

=  lim_x->1+ (x + 1)

=  2

f'(1^-)  =  1 and f'(1⁺)  =  2,  so the given function is not differentiable at x = 1.

After having gone through the stuff given above, we hope that the students would have understood, "Find the Derivatives From the Left and Right at the Given Point"

Apart from the stuff given in "Find the Derivatives From the Left and Right at the Given Point", if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.