FIND THE COORDINATES OF THE CENTRIOD OF A TRIANGLE WITH VERTICES

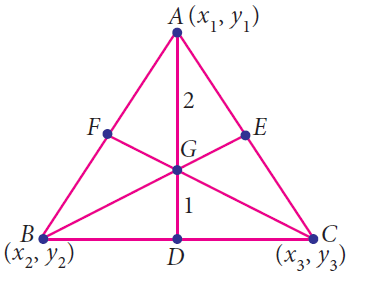
The centroid G of the triangle with vertices A(x₁, y₁), B(x₂ , y₂ ) and C(x₃ , y₃) is

  =  [ (x₁ + x₂ + x₃)/3, (y₁ + y₂ + y₃)/3 ]

In the above triangle , AD, BE and CF are called medians. All the three medians AD, BE and CF are intersecting at G. So  G is called centroid of the triangle 

Practice Questions

Question 1 :

Find the centroid of triangle whose vertices are (3, 4) (2, -1) and (4, -6).

Let the vertices be A (3,4) B (2,-1) and  C (4,-6)

x₁  =  3, x₂  =  2, x₃  =  4

y₁  =  4, y₂  =  -1, y₃  =  -6 

Centroid of a triangle = (x₁+x₂+x₃)/3, (y₁+y₂+y₃)/3

  =  [ (3+2+4)/3 , (4+(-1)+(-6)/3 ] 

  =  (5 + 4)/3 , (4 - 1 - 6)/3 

  =  [9/3 , (4-7)/3]   

  =  [9/3 , -3/3]   

  =  (3, -1)

Question 2 :

Find the centroid of triangle whose vertices are  (5, 6) (2, 4) and (1, -3).

Solution :

Let the vertices be A (5, 6) B (2, 4) and  C (1, -3)

x₁  =  5, x₂  =  2, x₃  =  1

y₁  =  6, y₂ = 4, y₃ = -3 

Centroid of a triangle = (x₁+x₂+x₃)/3, (y₁+y₂+y₃)/3

  =  [ (5+2+1)/3 , (6+4+(-3))/3 ]

  =  (7 + 1)/3 , (6 + 4 - 3)/3 

  =  [8/3 , (10-3)/3]   

  =  (8/3 , 7/3)

Question 3 :

Find the centroid of triangle whose vertices are  (1, 3) (-7, 6) and (5 ,-1).

Solution :

Let the vertices be A (1, 3) B (-7, 6) and  C (5, -1)

x₁  =  1, x₂ = -7, x₃  =  5

y₁  =  3, y₂  =  6, y₃  =  -1 

Centroid of a triangle = (x₁+x₂+x₃)/3, (y₁+y₂+y₃)/3

  =  [ 1 + (-7) + 5 ] / 3 , [ 3 + 6 + (-1) ] / 3

  =  (6 - 7)/3 , (3 + 6 - 1)/3 

  =  [-1/3 , (9-1)/3]   

 =  (-1/3 , 8/3)

Question 4 :

Find the centroid of triangle whose vertices are  (1, 1) (3, 4) and (5, -2).

Solution :

Let the vertices be A (1, 1) B (3, 4) and  C (5, -2)

x₁  =  1, x₂  =  3, x₃  =  5

x₁  =  1, x₂  =  4, x₃  =  -2

Centroid of a triangle = (x₁+x₂+x₃)/3, (y₁+y₂+y₃)/3

  =  [ (1+3+5)/3 , (1+4+(-2))/3 ]

  =  (4+5)/3 , (5-2)/3 

  =  (9/3 , 3/3)

  =  (3 , 1)

Question 5 :

Find the centroid of triangle whose vertices are  (-3, -9) (-1, 6) and (3, 9). 

Solution :

Let the vertices be A (-3,-9) B (-1,6) and  C (3,9)

x₁  =  -3, x₂  =  -1, x₃  =  3

y₁  =  -9, y₂  =  6, y₃  =  9 

Centroid of a triangle = (x₁+x₂+x₃)/3, (y₁+y₂+y₃)/3

  =  [ ((-3)+(-1)+3)/ 3 , ((-9)+6+9)/3 ]

  =  [-3 - 1 + 3 )/3 , (-9 + 6 + 9 )/3 

  =  [(-4 + 1)/3 , (-9 + 15)/3]   

  =  [-3/3 , 6/3]   

  =  (-1, 2)      

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.