FIND THE CONSTANT OF PROPORTIONALITY FROM A TABLE

Example 1 :

Examine the given table and determine if the relationship is proportional. If yes, determine the constant of proportionality.

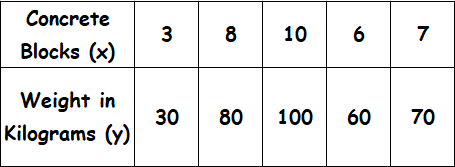
Solution :

Find the ratio of x and y for all the given values.

3/30 = 1/10

8/80 = 10

10/100 = 1/10

9/60 = 1/10

7/70 = 1/10

When we take ratio of x and y for all the given values, we get equal value for all the ratios.

Therefore, the relationship given in the table is proportional.

When we look at the above table when x gets increased, y also gets increased, so it is direct proportion.

Then, we have

y = kx

Substitute 3 for x and 30 for y.

30 = k(3)

10 = k

So, the constant of proportionality is 10.

That is, every concrete block weighs 10 kilograms.

Example 2 :

Examine the given table and determine if the relationship is proportional. If yes, determine the constant of proportionality. And also, explain what does the constant of proportionality mean?

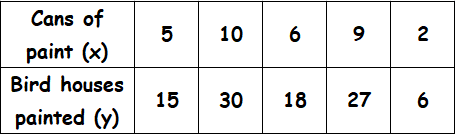
Solution :

Find the ratio of x and y for all the given values.

5/15 = 1/3

10/30 = 1/3

6/18 = 1/3

9/27 = 1/3

2/6 = 1/3

When we take ratio of x and y for all the given values, we get equal value for all the ratios.

Therefore, the relationship given in the table is proportional.

When we look at the above table when x gets increased, y also gets increased, so it is direct proportion.

Then, we have

y = kx

Substitute 5 for x and 15 for y.

15 = k(5)

3 = k

So, the constant of proportionality is 3.

That is, for every can of paint, you could paint 3 bird houses.

Example 3 :

Examine the given table and determine if the relationship is proportional. If yes, determine the constant of proportionality. And also, explain what does the constant of proportionality mean?

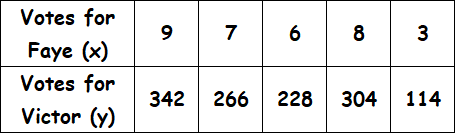
Solution :

Find the ratio of x and y for all the given values.

9/342 = 1/38

 7/266 = 1/38

6/228 = 1/38

8/304 = 1/38

3/114 = 1/38

When we take ratio of x and y for all the given values, we get equal value for all the ratios.

Therefore, the relationship given in the table is proportional.

When we look at the above table when x gets increased, y also gets increased, so it is direct proportion.

Then, we have

y = kx

Substitute 9 for x and 342 for y.

342 = k(9)

38 = k

So, the constant of proportionality is 38.

That is, for every vote for Faye there were 38 votes for Victor.

Example 4 :

Examine the given table and determine if the relationship is proportional. If yes, determine the constant of proportionality. And also, explain what does the constant of proportionality mean?

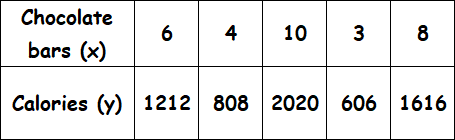
Solution :

Find the ratio of x and y for all the given values.

6/1212 = 1/202

4/808 = 1/202

10/2020 = 1/202

3/606 = 1/202

8/1616 = 1/202

When we take ratio of x and y for all the given values, we get equal value for all the ratios.

Therefore, the relationship given in the table is proportional.

When we look at the above table when x gets increased, y also gets increased, so it is direct proportion.

Then, we have

y = kx

Substitute 6 for x and 1212 for y.

1212 = k(6)

202 = k

So, the constant of proportionality is 202.

That is, every chocolate bar has 202 calories.

Example 5 :

Examine the given table and determine if the relationship is proportional. If yes, determine the constant of proportionality. And also, explain what does the constant of proportionality mean?

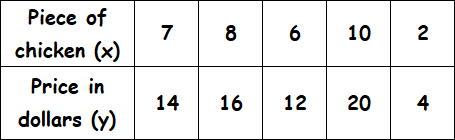
Solution :

Find the ratio of x and y for all the given values.

7/14 = 1/2

8/16 = 1/2

6/12 = 1/2

10/20 = 1/2

2/4 = 1/2

When we take ratio of x and y for all the given values, we get equal value for all the ratios.

Therefore, the relationship given in the table is proportional.

When we look at the above table when x gets increased, y also gets increased, so it is direct proportion.

Then, we have

y = kx

Substitute 6 for x and 1212 for y.

1212 = k(6)

202 = k

So, the constant of proportionality is 202.

For each piece of chicken it costs 2 dollars.

Example 6 :

Examine the given table and determine if the relationship is proportional. If yes, determine the constant of proportionality. And also, explain what does the constant of proportionality mean?

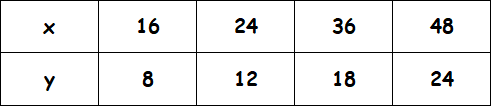
Solution :

Find the ratio of x and y for all the given values.

16/8 = 2

24/12 = 2

12/6 = 2

20/10 = 2

4/2 = 2

When we take ratio of x and y for all the given values, we get equal value for all the ratios.

Therefore, the relationship given in the table is proportional.

When we look at the above table when x gets increased, y gets decreased, so it is inverse proportion.

Then, we have

y = k/x

Substitute 16 for x and 8 for y.

8 = k(16)

1/2 = k

So, the constant of proportionality is 1/2.

Example 7 :

Examine the given table and determine if the relationship is proportional. If yes, determine the constant of proportionality. And also, explain what does the constant of proportionality mean?

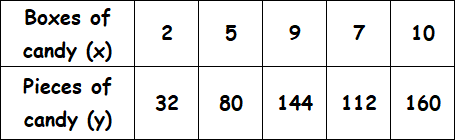
Solution :

Find the ratio of x and y for all the given values.

2/32 = 1/16

5/80 = 1/16

9/144 = 1/16

7/144 = 1/16

10/160 = 1/16

When we take ratio of x and y for all the given values, we get equal value for all the ratios.

Therefore, the relationship given in the table is proportional.

When we look at the above table when x gets increased, y gets decreased, so it is inverse proportion.

Then, we have

y = kx

Substitute 2 for x and 32 for y.

32 = k(2)

16 = k

So, the constant of proportionality is 16.

That is, for every box of candy you get 16 pieces.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.