FIND THE CAPACITY OF FOLLOWING FIGURES
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
What is volume ?
The amount of space occupied by an object is called its volume.
To measure volume we can use the following units :
- cubic centimeter (cm3)
- cubic meter (m3)
What is capacity ?
The amount that a container can hold is called capacity.
capacity can be measured using the units :
- Milliliters (ML)
- Liter (L)
- Kiloliter (KL)
Relationships involving units of volume and capacity are given below.
1 cm3 = 1 ML
1000 cm3 = 1 L
1 m3 = 1 KL
Conversion and basic operations involving units of volume and capacity can be worked out using the relations given above.
Find the capacity (in KL) of the following tanks.
Problem 1 :
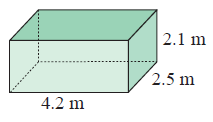
Solution :
By observing the figure, it is a rectangular tank.
Here the area of cross-section is the shape of the rectangle.
To find the volume,
Volume = area of cross-section × height
= area of rectangle × height
= length × width × height
we have,
length = 4.2 m, width = 2.5 m and height = 2.1 m
= 4.2 × 2.5 × 2.1
Volume = 22.1 m3
To find the capacity,
1 m3 = 1 KL
Capacity = 22.1 KL
So, the capacity of the tank is 22.1 KL.
Problem 2 :
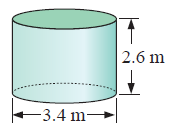
Solution :
By observing the figure, it is a cylindrical tank.
Here the area of cross-section is the shape of the circle.
To find the volume,
Volume = area of cross-section × height
= area of circle × height
= πr2 × height
we have,
diameter = 3.4 m and height = 2.6 m
radius = 3.4/2 = 1.7 m
= π(1.7)2 × 2.6
Volume = 23.6 m3
To find the capacity,
1 m3 = 1 KL
Capacity = 23.6 KL
So, the capacity of the tank is 23.6 KL.
Problem 3 :
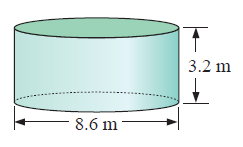
Solution :
By observing the figure, it is a cylindrical tank.
Here the area of cross-section is the shape of the circle.
To find the volume,
Volume = area of cross-section × height
= area of circle × height
= πr2 × height
we have,
diameter = 8.6 m and height = 3.2 m
radius = 8.6/2 = 4.3 m
= π(4.3)2 × 3.2
Volume = 186 m3
To find the capacity,
1 m3 = 1 KL
Capacity = 186 KL
So, the capacity of the tank is 186 KL.
Problem 4 :
A new perfume in a 36mm (internal) diameter spherical bottle comes on to the market.
a) Calculate the capacity of the bottle in mL.
b) If the bottle costs $25 and the bottle and its contents cost $105, how much does the perfume cost per mL ?
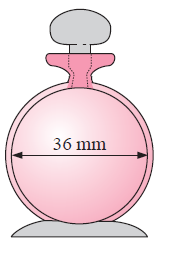
Solution :
a)
Given diameter = 36 mm of spherical ball.
radius (r) = 36/2 = 18 mm
By converting mm to cm, we get
1 mm = 1/10 cm
18 mm = 18/10 cm
radius (r) = 1.8 cm
To find the volume,
Volume of sphere = 4/3πr3
= 4/3π(1.8)3
Volume = 24.4 cm3
To find the capacity,
1 cm3 = 1 mL
Capacity = 24.4 mL
So, the capacity of the bottle is 24.4 mL.
b)
Cost of the bottle = $25
Cost of the contents = $105
Total cost of the perfume = cost of the contents - cost of the bottle
= $105 - $25
Total cost = $80
Cost of the perfume per mL = Total cost of the perfume/capacity of the perfume
= $80/24.4
= $3.27 per mL
Problem 5 :
Which container of orange juice would give the better value :
A) a cylindrical bottle of diameter 16 cm and height 19.9 cm costing $5.75 (or)
B) a rectangular cask measuring 20 cm by 15 cm by 10 cm costing $4.50 ?
Solution :
A)
Given, diameter = 16 cm and height = 19.9 cm
radius (r) = 16/2 = 8 cm
To find the volume,
Volume of cylinder = πr2h
= π(8)2 × 19.9
Volume = 3999.1 cm3
To find the capacity,
1000 cm3 = 1 L
(3999.1)/1000 = 4 L
Capacity = 4 L
So, the capacity of the cylindrical bottle is 4 L.
cost of the cylindrical bottle = $5.75
The value of orange juice in the cylindrical bottle = Cost of the cylindrical bottle/capacity
= $5.75/4
= $1.44 per litre
B)
Given, length = 20 cm, width = 15 cm and height = 10 cm
To find the volume,
Volume of rectangle = length × width × height
= 20 × 15 × 10
Volume = 3000 cm3
To find the capacity,
1000 cm3 = 1 L
(3000)/1000 = 3 L
Capacity = 3 L
So, the capacity of the rectangular cask is 3 L.
cost of the rectangular cask = $4.50
The value of orange juice in the rectangular cask = Cost of the rectangular cask/capacity
= $4.50/3
= $1.5 per litre
A) The value of orange juice in the cylindrical bottle is $1.44 per litre.
B) The value of orange juice in the rectangular cask is $1.5 per litre.
Therefore, A is better value.
Problem 6 :
A roof has surface area of 110 cm2 and one night 12 mm of rain falls on the roof. All the water goes into a tank of base diameter 4 m.
a) Find the volume of water which falls on the roof.
b) How many KL of water enter the tank ?
c) By how much will the water level rise in the tank ?
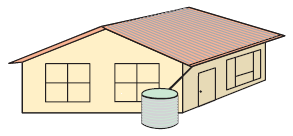
Solution :
a)
Given, Area = 110 cm2, Rainfall = 12 mm
By converting mm to m, we get
(12)/1000 = 0.012 m
Rain depth = 0.012 m
Volume of water that fell on the roof = Area × Rain depth
= 110 × 0.012
Volume = 1.32 m3
b)
1 m3 = 1 KL
1.32 m3 = 1.32 KL
So, 1.32 KL of water enters the tank.
c)
diameter = 4 m, radius = 2 m
Volume of cylindrical tank = πr2h
= π(2)2h
= 4πh
The volume added to the tank must be equal to the volume which falls on the roof.
Volume of tank = volume of water that fell on the roof
4πh = 1.32
h = 1.32/4π
h = 0.10504 m
= (0.10504 × 100) cm
h = 10.5 cm
So, the water level rises in the tank by about 10.5 cm.
Problem 7 :
A motor car has a rectangular prism petrol tank 48 cm by 56 cm by 20 cm. If the car consumes petrol at an average rate of 8.7 litres per 100 km, how far could it travel on a full tank of petrol ?

Solution :
Given, length = 48 cm, width = 56 cm and height = 20 cm
Volume of rectangular tank = length × width × height
= 48 × 56 × 20
Volume = 53760 cm3
To find the capacity,
1000 cm3 = 1 L
(53760)/1000 = 53.76 L
Capacity of the petrol tank = 53.76 L
For 8.7 litre car goes = 100 km
For 53.76 litre car goes = (53.76)/8.7 × 100
= 618 km
So, the car can travel 618 km with a full tank of petrol.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
10 Hard SAT Math Questions (Part - 45)
Jan 19, 26 06:14 AM
10 Hard SAT Math Questions (Part - 45) -
10 Hard SAT Math Questions (Part - 44)
Jan 12, 26 06:35 AM
10 Hard SAT Math Questions (Part - 44) -
US Common Core K-12 Curricum Algebra Solving Simple Equations
Jan 07, 26 01:53 PM
US Common Core K-12 Curricum Algebra Solving Simple Equations
