FIND THE AREA OF A PARALLELOGRAM FORMED BY VECTORS

In this section, you will learn how to find the area of parallelogram formed by vectors.

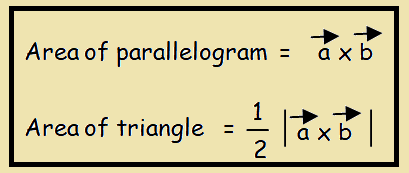
Practice Problems

Problem 1 :

Find the area of the parallelogram whose two adjacent sides are determined by the vectors i vector + 2j vector + 3k vector and 3i vector − 2j vector + k vector.

Solution :

Let a vector  =  i vector + 2j vector + 3k vector

b vector  =  3i vector − 2j vector + k vector.

Vector area of parallelogram  =  a vector x b vector

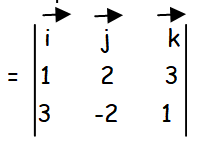
  =  i[2+6] - j[1-9] + k[-2-6]

  =  8i + 8j - 8k

  =  √8² + 8² + (-8)²

  =  √(64+64+64)

  =  √192

  =  8√3 square units

Problem 2 :

Find the area of the triangle whose vertices are A(3, - 1, 2), B(1, - 1, - 3) and C(4, - 3, 1).

Solution :

A vector  =  (3i - j + 2k) vector

B vector  =  (i - j - 3k) vector

C vector  =  (4i - 3j + k) vector

AB vector  =  -2i vector -5k vector

AC vector  =  i vector - 2j vector - k vector

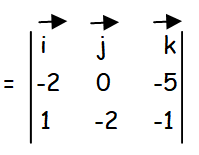
  =  i[0-10]-j[2+5]+k[4-0]

  =  -10i+7j-4k

Area of triangle =  (1/2) |AB vector x AC vector|

  =  (1/2) √(-10)² + 7² + (-4)²

  =  (1/2) √(100+49+16)

  =  (1/2) √165

So, the area of the given triangle is (1/2) √165 square units.

Problem 3 :

If a vector, b vector, c vector are position vectors of the vertices A, B, C of a triangle ABC, show that the area of the triangle ABC is (1/2) |a × b + b × c + c × a| vector. Also deduce the condition for collinearity of the points A, B, and C.

Solution :

Let OA vector  =  a vector

OB vector  =  b vector

OC vector  =  c vector

Area of triangle ABC  =  (1/2) |AB vector x AC vector|

  =  (1/2) |(OB - OA) x (OC - OA)|

  =  (1/2) |(b - a) x (c - a)|

  =  (1/2) |(b x c - b x a - a x c + a x a)|

  =  (1/2) |(b x c + a x b + c x a + 0 vector)|

  =  (1/2) |a x b + b x c + c x a|

If the points A, B and C are collinear, then 

Area of triangle ABC  =  0

(1/2) |a x b + b x c + c x a|  =  0

|a x b + b x c + c x a|  =  0

a x b + b x c + c x a  =  0

So, the required condition is 

a x b + b x c + c x a  =  0

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.